by Shawn Burke, Ph.D.
Introduction
Statistics for the Science of Paddling blog show that one of the most popular posts is Part 3: The Rough Stuff. In that post, we consider how friction drag arises over our hulls. And when I chat with fellow paddlers about “science stuff,” one of the first things they zero in on is how to reduce friction drag. Which tells me my work here isn’t done.
Why? Because the drag force acting on our hulls comprises three parts: form drag, wave-making drag, and friction drag. Friction drag is just a part of the overall picture. Its contribution to total drag pales compared to the others for paddling speeds above a couple of miles per hour.
So, in this installment of The Science of Paddling, we’ll weave together the loose skeins from several other posts to understand the total drag for acting on our hulls. We’ll do this using Newton’s Laws of Motion, written in their original form, plus conservation of energy. We’ll conclude with a thought experiment: Would a heavier competitive paddler benefit from choosing a longer hull?
Let’s start by paying Isaac Newton a visit.
The Laws of Motion
In 1687 Newton published his discoveries about forces and their role in the motion of bodies and planets. The most well-known elements of his book are the three Laws of Motion. These axioms describe phenomena we routinely observe in the world around us. They also apply to everything that happens when we’re in a paddled hull. We’ll review the Laws very briefly, then apply them to understand each component of total drag. This will allow us to address my friend’s question.
The 1st Law states:[1]
Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed.
This implies that a canoe, kayak, SUP, outrigger, dragon boat, etc. will remain stationary or move at a constant speed unless an external force is applied.
From experience, we know that if we apply a forward paddling stroke, the hull no longer moves at a constant speed – including a “constant speed” of zero – but will instead speed up. The force of the paddling stroke “compels” the hull to “change its state” from one speed to another.
We also know from experience that, on quiet water, a hull slows down when we stop paddling. This is because drag forces are “impressed” upon the hull, constantly changing its state from one speed to another.
The 2nd Law states:
A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.
In the 2nd Law, motion means momentum, the product of an object’s mass and velocity. Consequently, a change in an applied force, such as that delivered over a paddle stroke, changes the momentum of the hull/paddler system in the direction of propulsion. The 2nd Law also helps us understand form drag, which we’ll revisit below.
The 3rd Law states:
To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.
Here, “action” means force. The second half of the 3rd Law encompasses orbiting celestial bodies, billiard balls bouncing off each other, and objects in static equilibrium – like you sitting in your chair reading this.
We’ll add a later discovery to Newton’s Laws, attributed to James Prescott Joule: conservation of energy. Joule found that mechanical, electrical, and heat energy are fundamentally the same thing in different forms. While energy can be exchanged within a bounded system over time, the system’s total energy remains constant. We relied on this to deduce why hulls create wave trains in Part 4: Shallow Water. We’ll use the principle extensively below.
The Forces Acting on a Hull
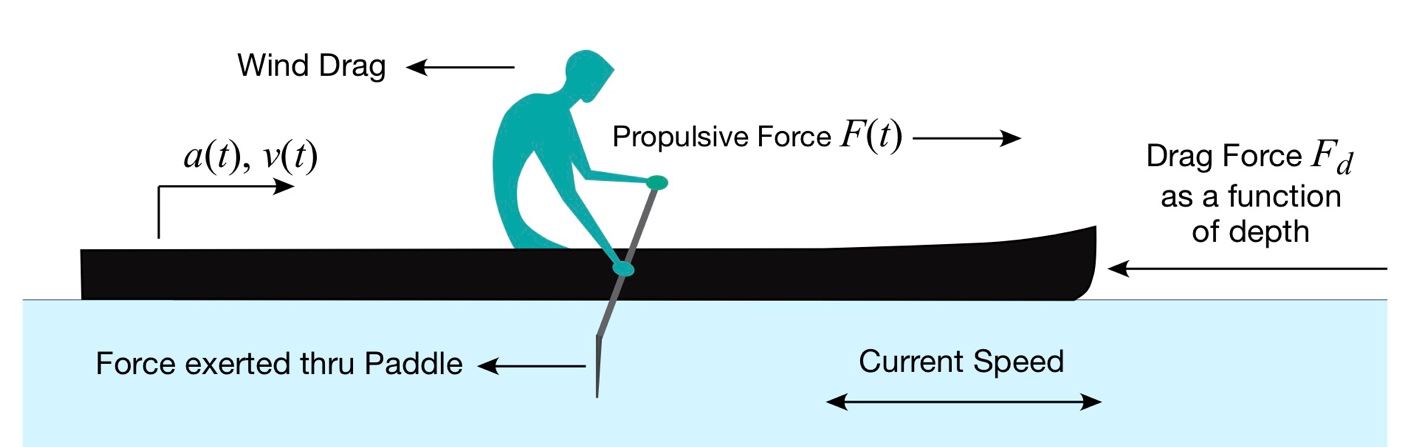
Figure 1: Paddle, hull, and various forces.
Consider now the hull depicted in Fig. 1. Various forces are “impressed” upon it. First, the paddle force and its corresponding reaction, the propulsive force, co-arise due to Newton’s 3rd Law. The propulsive force changes our hull’s momentum, and speeds it up or slows it down because of Newton’s 2nd Law. A wind-induced drag force acts on the hull above the waterline, and on the paddler’s body, slowing it down (“changes the state”) because of Newton’s 1st and 2nd Law. And finally, a drag force Fd slows it owing to Newton’s 1st and 2nd Laws. We’ll restrict ourselves to just the drag force Fd for the ensuing discussion.
Let’s examine each of Fd’s components and their genesis.
Friction Drag
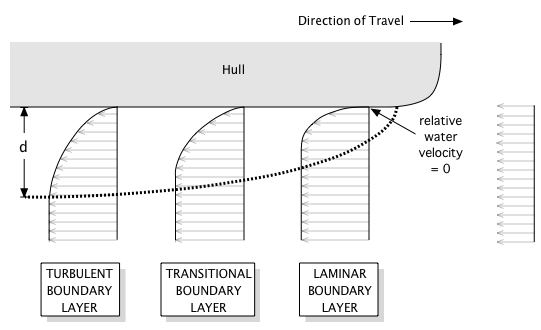
Figure 2: Boundary Layer Development.
The first of the three drag force components is friction drag. Many people think this is the only type of drag acting on a hull. It’s not. But friction drag is the easiest to understand.
As our hulls glide over the water, the fluid at the hull’s surface “sticks” there. This phenomena is called the no-slip condition. If we adopt a frame of reference centered in the hull, the water appears to move past us at our paddling speed. Let’s call that speed U. Below the waterline, the relative speed between the hull and water must equal zero at the hull’s surface. Consequently, there must be a transition region for the water to “catch up” with the free-stream speed U. This region is called the boundary layer, illustrated in Fig. 2.
Immediately adjacent to the hull’s surface, the physics is dominated by diffusion owing to shear stresses, e.g., friction. This holds true across the laminar portion of the boundary layer. As you move further away from the hull, and along the hull’s length, the boundary layer is dominated by vortex generation – turbulence. These energetic processes are the genesis of friction drag. And they are fed by you, the paddler, because the hull is moving through a fluid. The total system energy is conserved within the control volume encompassing the hull and the boundary layer. Friction drag is merely transforming energy from your motion into the boundary layer, thus slowing you down.
For more details on friction drag, visit Part 3: The Rough Stuff.
Wave Drag
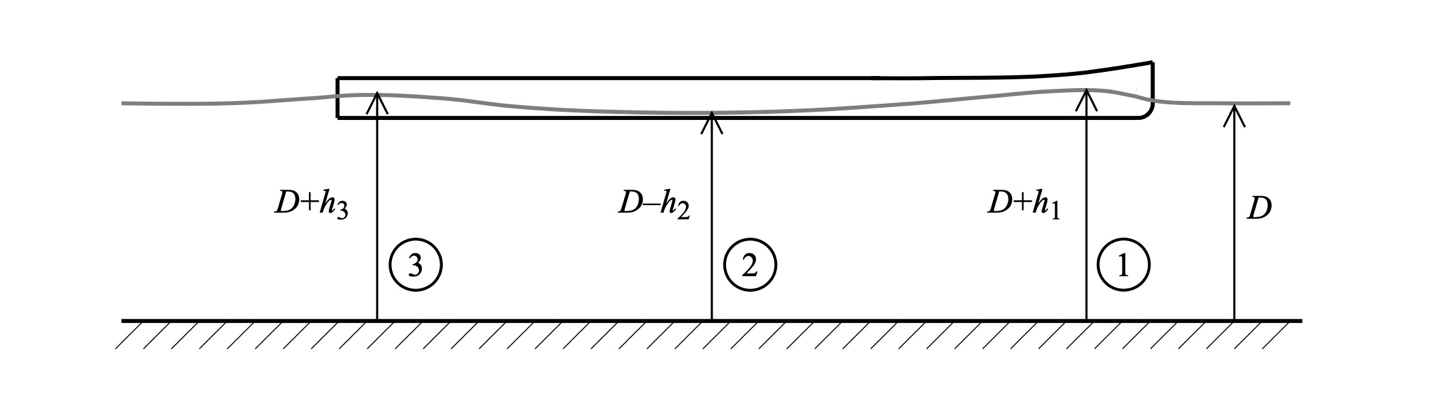
Figure 3: Wave generation alongside a hull.
The second of the three drag force components is wave drag. Wave drag arises because of the change in the water’s kinetic energy as it encounters your hull. This is illustrated in Fig. 3.
We’ll assume once again that our hull is moving at speed U. If we adopt a hull-centered frame of reference, then from our perspective the water is flowing toward our hull at the speed U. When the water first strikes the hull at the bow, it immediately slows down, as if its kinetic energy hit a solid object – which it did. The water piles up near the bow, rising above the average water depth D as shown in the figure at location ‘1’. This increase in height h1 locally raises the water’s potential energy, much like throwing a ball in the air raises the ball’s potential energy. Since the energy in the hull/water system is conserved, further along the hull the water’s surface drops below the average depth D by an amount h2, where there is less potential energy than at location ‘1’ but greater kinetic energy. This wave-like pattern alongside the hull creates waves that radiate outward, as shown in Fig. 4.
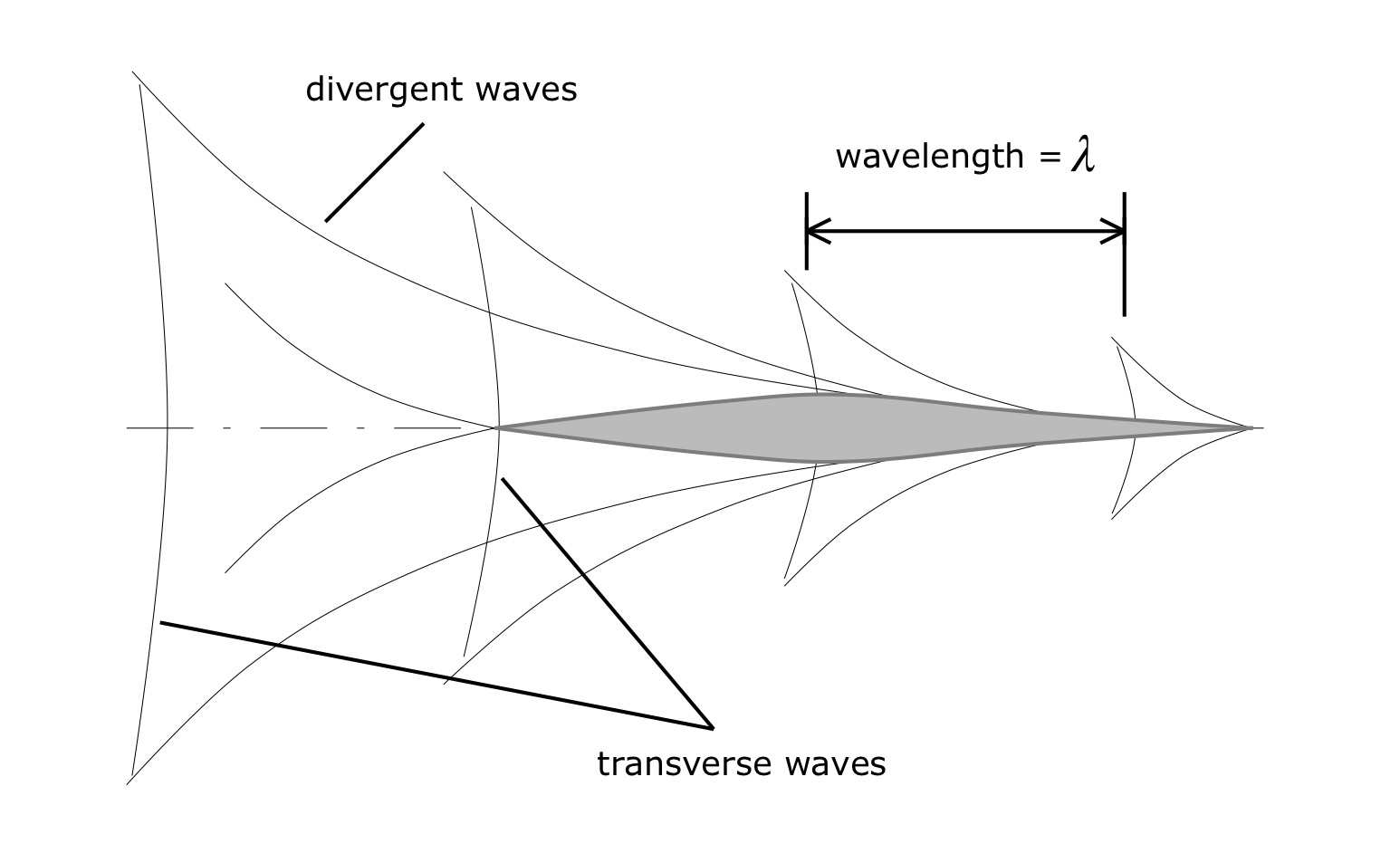
Figure 4: Froude-Kelvin wavetrain propagating from a hull.
We can trace the potential and kinetic energy in the wavetrain to its source: the kinetic energy of the incoming flow. But when we “undo” our coordinate transformation and return to an inertial (Earth-centered) frame of reference, we see that the speed U generating the kinetic energy to feed the waves comes not from the flow but from you, the paddler. If our hull were not present, there would be no Froude-Kelvin wavetrain. We create it by our movement over the water’s surface. And that wave energy continues to radiate outwards as we paddle. We are its fuel.
The specifics of the wavetrain are also driven by hull design. Some sleek hulls produce comparatively low amplitude waves. By contrast, my C-4 canoe generates transverse waves that every other paddler wants to sit in. But the waves will be there, no matter what. Far enough away from the hull, the wave crests will diverge in a fan-shaped pattern with asymptotes angled 18.6 degrees. Kelvin-Froude waves are a property of the water’s surface; they’re just Nature happening.
Form Drag
Hold your hand out in front of you, arm fully extended, with the palm held horizontal. Now briskly swing your hand side-to-side while keeping your arm straight. Notice the force exerted on your hand. Next, repeat the experiment, but rotate your hand so the palm is oriented vertically. Notice the force exerted on your hand. The effect is more dramatic if you hold your hand out a car window while driving (just be careful). So why are the forces on your hand different for these two orientations?
As we saw in Part 1: Tandem vs. Solo, friction drag is proportional to the hull’s wetted surface area below the waterline. In your “hand as a hull” experiment, the hand was fully immersed in a fluid – air – in both orientations. And the hand’s surface area didn’t change. An analysis based on surface friction alone would predict no change in drag between the two orientations. However, the size and shape of the wake behind your moving hand are different.
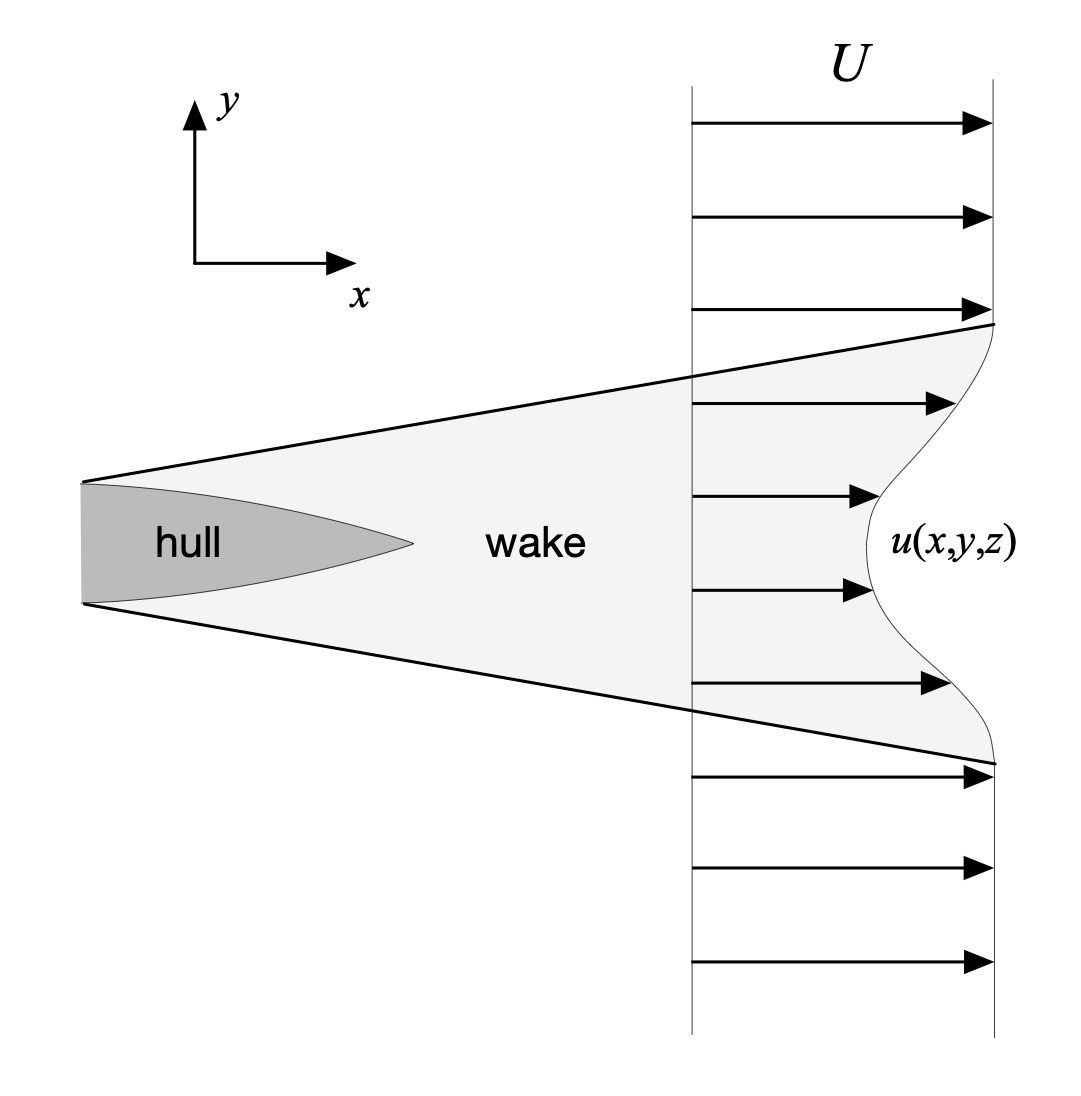
Figure 5: Wake, plan view.
Now consider a hull moving at speed U and its wake as depicted in Fig. 5. We’ll again adopt a reference frame centered on the hull. As we learned in Part 26: Waking Up, the wake behind a moving hull reflects a change in the incoming water’s momentum. On average, the flow speed in the wake u is less than the free-stream flow speed U. Consequently, the water, which has mass, has a lower momentum inside the wake than outside it. This change in momentum exerts itself as the form drag force on the hull.
This is a consequence of Newton’s 2nd Law, which reads in part, “[a] change in [momentum] is proportional to the motive force impressed.” The reverse also holds true: a change in momentum impresses a force. You’ve experienced this if you’ve ever ridden in a decelerating car. Decelerating means changing the car’s momentum, which leads to a force that makes you pitch forward in your seat. Here, the change is the difference between the water’s momentum at speed U if no hull were there versus the momentum when the hull is present. Once again, the system’s energy – the fluid’s kinetic or motion energy – is conserved. The energy is redistributed from the unimpeded upstream flow into the wake’s flow, typically including vortices and other fun structures.
Form drag is a property of the wake. The larger the wake, the greater the form drag. This is where apt hull designers earn their keep since the hull shape influences the size of the wake.
Now let’s bring all these tools to bear and consider our heavier paddler.
A Thought Experiment
Should a heavier paddler move from a first hull of a certain length to a longer hull? A friend asked me this question the other day, and it got me thinking. Like many things in life, the answer is, “it depends.” In this section, we’ll consider arguments for and against changing hulls in light of what we’ve learned about Newton’s Laws, the three components of drag, and energy. We’ll start by reviewing the role weight plays in our hulls.
We experience Newton’s 3rd Law when we place one of our hulls in the water. The hull floats. This is because the hull displaces a volume of water, leading to a buoyancy force that precisely equals the hull’s weight. The buoyancy force acts upward, while the weight of the hull acts downward in the direction of gravity’s pull. When we climb aboard, the hull sinks lower, displacing an additional volume of water whose weight equals our weight. If we remain afloat, these opposing forces – buoyancy and weight – balance each other. Our weight is the “action,” while the buoyant force is the equal and opposite “reaction.” We learned this in Part 19: Roll Your Boat, while investigating our hulls’ roll stability.
If you place more weight in the hull, like paddles, lunch, and a drink jug, the hull sinks further into the water. Add in a loaded pack or two, and it sinks even further. So clearly, the greater the weight, the lower the hull sits in the water. And if we moved that same weight into a hull with a different design but the same empty weight, the volume of water displaced by this second hull would be the same. This is a consequence of Archimedes’ Principle.
The difference between these two hulls might be their shape below the waterline: length, beam, hard or soft chines, asymmetric width fore-and-aft about midships, etc. Certainly, the displaced volume must be the same in both cases. But the wetted area might be different because of the different hull shapes.
For example, we can prove[2] that the 3D shape having the smallest surface area to volume ratio is a sphere. A cube of the same volume has a 24.1% greater surface area. For a given volume, an object’s shape determines its surface area. The same goes for our hulls. As we learned above, friction drag force is proportional to the wetted area. Moving from a first hull into a longer hull might change the wetted area.
Designers specify a hull’s nominal waterline to characterize its stability and performance. For example, this waterline will be set for a target paddler weight. The hull will sink further in the water if a paddler exceeds this weight. This increases the hull’s cross-sectional area below the waterline, which increases drag, as we learned in Part 1: Tandem vs. Solo. As expected, a greater cross-sectional area below the waterline leads to a larger wake. How much larger depends on the hull’s morphology, a fancy word for “shape.” And a greater wake deficit leads to increased form drag.
Any change in wave-making drag will depend on the two hulls’ designs; it’s difficult to generalize. However, a longer hull will have a greater hull speed: the “natural” top-end speed[3] in deep water where the hull fits inside one surface wave wavelength. As we learned in Part 4: Shallow Water, the hull speed varies as the square root of waterline length. So, to first order, a longer hull will be a faster hull, all other things being equal, and that advantage goes as the square root of waterline length.
As we learned in Part 14: Kind of a Drag, a hull’s performance can be represented partly by its drag coefficient CD. The drag coefficient reflects the hull’s total drag. Consequently, CD depends on the hull’s wetted area and wave- and wake-generating characteristics under specified operating conditions of depth (e.g., paddler weight) and trim. Ideally, manufacturers would list their hulls’ drag coefficients for various paddler weights. Unfortunately, we don’t live in that world. But if we did, the answer to my friend’s question would be simple. For a paddler of a given weight, the hull with the lowest CD at that operating weight would be the fastest. As we’ve seen from our analysis, absent that information, the best we can tell my friend is, “it depends.”
Summary
In this installment of the Science of Paddling series, we reviewed the three components of the total drag force acting on our hulls: friction drag, wave drag, and form drag. At the risk of sounding like a broken record, the total drag force comprises all three components, not just friction drag. We reviewed each and saw how they are embodiments of Newton’s Laws of Motion. Add a dash of Joule’s conservation of energy, and we have bounded the drag problem.
As to my friend and his question of whether a longer hull would suit a heavier paddler, there is no simple way to answer this. Further, considering my experience, a nominally faster hull may be slower. I remember the first time I climbed into a Wenonah J-200 solo racing canoe. I was not a happy camper. Granted, I had come from a canoe-tripping background where Old Town ‘Tripper’ hulls were the norm. Yet even now, I find the J-200 too twitchy for me. Unless you are comfortable in a hull, you won’t feel confident “putting the charcoal to it” and achieving its full potential.
© 2023, Shawn Burke, all rights reserved. See the Terms of Use for more information.
- The translations of the laws of motion used here are from Bernard Cohen and Anne Whitman, The Principia: Mathematical Principles of Natural Philosophy, University of California Press, Oakland, California (1999) ↑
- This is a problem you’ll often encounter in a 2nd-year calculus course. ↑
- Lest you send me a flurry of cards and letters disputing this, let me preemptively say that I agree. A hull’s top-end speed will generally be slightly above the hull speed, and fitter and more skilled paddlers will be able to exceed it. ↑
