by Shawn Burke, Ph.D.

INTRODUCTION

I recently received an email asking if there was a way to quantify a paddler’s performance in an OC-6 outrigger in comparison to their teammates. In other words, was there a way that science could be leveraged to determine whether a paddler was equal to, lesser, or greater than the other paddlers in a boat. Using an analogy from baseball, is there something like “Wins Above Replacement” (aka, “WAR”) for paddling? Would such a tool be useful for filling out teams for outrigger or dragon boat racing? Or could it be used to determine which seat is best for a paddler in a C4?

Sure; there’s a way to quantify this. But first, let’s address the elephant in the room. Lurking beneath this question are issues of fairness, team building, as well as inter-personal dynamics and conflicts if we’re addressing team selection. Physics doesn’t have anything to say about those hot button issues; they are best left to coaches and sports psychologists. In what follows we’ll assume that everyone plays nice and are imbued with an abundance of equanimity. Your mileage may vary.

Given that overarching caveat, what is paddling’s version of WAR? Turns out there’s an obvious choice that’s readily measured in the field. And it all hinges on what we learned in Part 1 of the Science of Paddling.

SPEED VS. POWER IN THE BOAT

As you may recall from Part 1, the speed of a paddled hull is proportional to the cube root of the applied paddling power. Most generally, for a hull having N paddlers this is expressed as

where v_N is the speed of an N-paddler hull, c_N combines all of the hydrodynamic aspects of the N-paddler hull into a single constant (like we’ve done in previous articles), and P_i is the power generated by each of paddlers 1 to N. For an OC-6 this can be written somewhat laboriously as

and for a C4 it can be written as

We needn’t worry about the particulars of the hydrodynamics constants, for reasons that will soon become clear.

First, let’s consider the C4 case. In Fig 1 we depict a C4 being paddled from left to right. In the first case paddlers in all four seats are paddling, represented by green seats (which are easier to draw than green paddlers!). We assume that the hull has been brought up to speed and is moving at a steady pace over flat water with no current. In the second case the paddler in the 2^nd seat has stopped paddling – hence the red seat – and is sitting upright in their seat. They have also feathered their paddle so as not to introduce any air drag from their paddle blade.

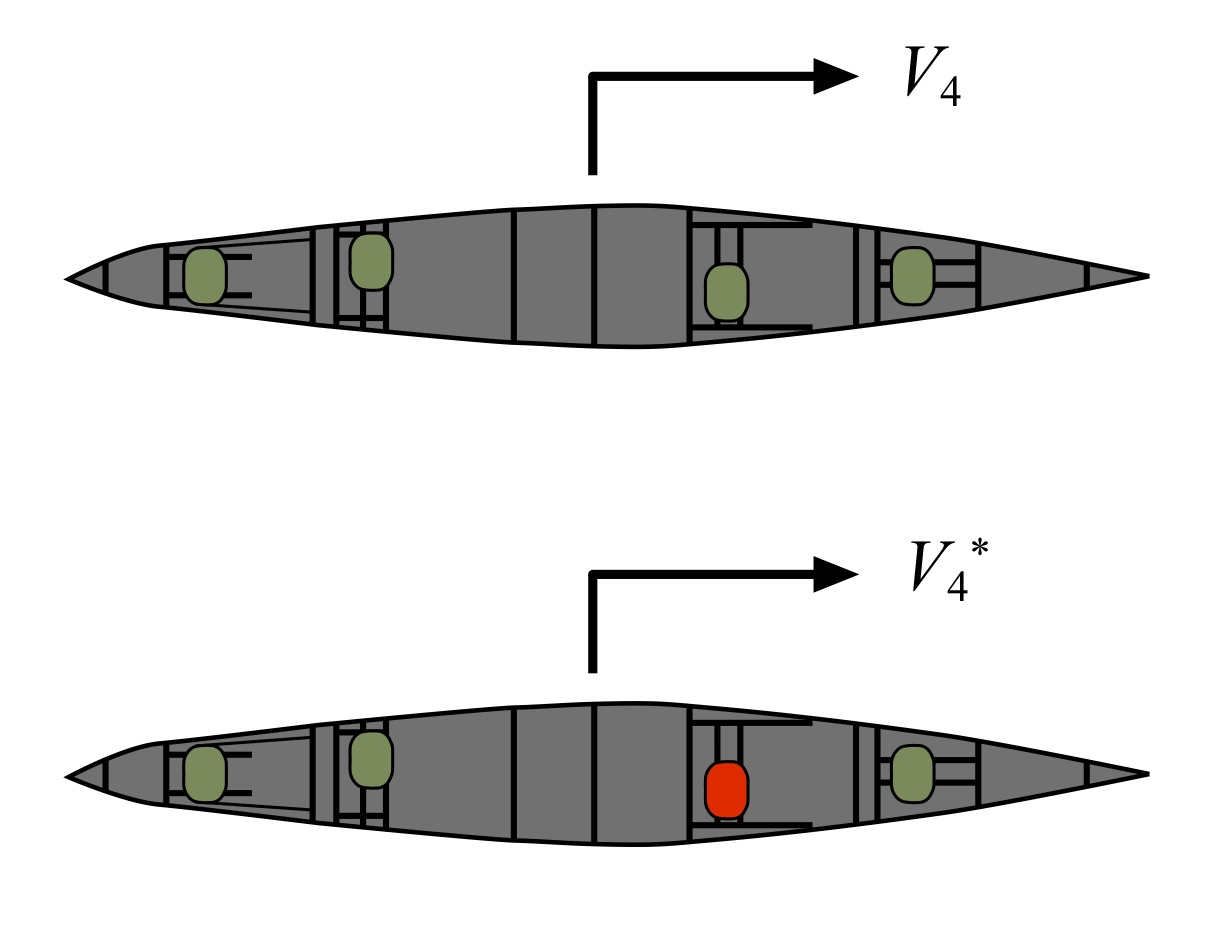
Fig. 1: C4 case, no current.

The hull speed for the first case was already presented above. For the second case,

where v₄^* denotes the hull speed with one paddler – in this case, the second – offline. In principle this could represent seats 1 through 4 going offline, but in practice taking the stern paddle off would be problematic since they call may switches, etc.

The ratio of hull speeds for these two cases is

Note that by taking a ratio the hydrodynamic coefficient c_N is cancelled out. One less thing to worry about! Since we are interested in quantifying (in this case) paddler 2 compared to the other 3 paddlers in the hull, we’ll assume that the other paddlers all exert the same paddling power P. We’ll also assume that in the baseline case where all 4 paddlers are engaged that paddler 2’s applied power isn’t too different from this average power P; we’re interested in determining how they differ from this average. As a result, the impact of taking paddler 2 offline can be quantified via the ratio

If paddler 2 can apply the same average power as their teammates, then the ratio of hull speeds for these two cases should be about 1.1, e.g. the C4 moves 10% faster when paddler 2 is paddling vs. when they are not (and are still in the boat). If the speed ratio is great than this, paddler 2 was applying more power than the average, and thus is above average in comparison to their teammates. If the hull speed ratio is less than this, paddler 2 was applying less power than the average, and is thus below average in comparison to their teammates. We’ll call this the C4 Speed Above Replacement (“SAR”) threshold of a paddler for that complement of paddlers. It does not apply in comparison to all paddlers (e.g., including everyone not in the boat) since it would require measurements of all paddlers in that same hull for comparison; not very practical.

For an OC-6,

which for the uniform baseline power assumption reduces to

This is the OC-6 SAR threshold for a paddler in comparison to their teammates.

One sees that as the number of paddlers increases above 6, this ratio will get smaller. Since the speeds used to compute the ratio in the field are subject to measurement error this indicates that for some number of paddlers N the SAR threshold ratio will approach 1 and thus fall below the measurement error^[1]. Consequently, the SAR approach outlined here will be of little if any utility for, say, dragon boaters.

There are many simplifying assumptions inherent in this analysis that have to be taken into account if you wish to measure SAR in a field test. In the words of acoustician Richard Bolt, we need to salt our analysis with liberal doses of common sense. First, taking a paddler offline means that the hull first has to stabilize to a new speed powered by the balance of the crew before gathering the speed data used to compute SAR. As we saw in Part 14:Kind of a Drag, it takes the better part of a minute for a C-1 to go from 1 paddler to no paddlers and have its speed stabilize (in that case, drop to zero). An on-water assessment needs to incorporate not only an accelerating interval up to a uniform baseline speed, but a stabilization time to account for the hull decelerating to its new speed. Further, it would be best to determine the two speeds used in the SAR calculation as an average over a finite time interval after speed stabilizes, say a minute or two. Next, the hull needs to either be paddled in deep water so there are no shallow water effects, or in water with uniform depth over the test range, or data needs to be averaged over a test range paddled in both directions so as to account for depth variations in the test course where the speed data used to compute SAR is acquired.

Taking a paddler offline in the 2^nd or 3^rd seat of a C4 may be comparable; comparing seat 2 to seat 1 is perhaps a bit more problematic in light of each of those seat’s respective access to the water. If would be best in that case to conduct tests that swap paddlers among seats to remove any inherent biomechanical bias.

Probably the most important test parameter is accounting for the other paddlers’ possible inclination to either speed up or slow down when one paddler goes offline. Aside from accounting for human nature (see the qualifier above about sports psychologists), maintaining uniform applied power from the other paddlers in both cases can be challenging. Asking each paddler to maintain the same RPE (Rating of Perceived Effort) while paddling is a possibility. Alternatively, asking them to maintain a uniform heart rate as presented on a heart rate monitor (HRM) during the test (after a thorough warmup so as to account for heart rate drift) is probably a better control than RPE; heart rate data can be reviewed post-test to ensure this constraint was met. All that being said, there are a fair number of things to control for in order to ensure this means of assessment is done repeatably and fairly.

IMPACT OF CURRENT

In the analysis above we did not account for environmental factors such as current and wind. For C4 and OC-6 paddlers you may be able to find a day or time to conduct this test with little or no wind. But to ask for a test range with no current? That could be a good deal more challenging for an OC-6.

Assuming that current doesn’t change over the time needed to make the necessary averaged speed measurement described below, one can still conduct the test. Consider again the C4 case (since I’ve already drawn it for the no-current case), as shown in Fig. 2. The C4 is being paddled left-to-right in the presence of a uniform current having speed v₀. Consequently, when the C4 is paddled with the current its speed over ground is now v₀ + v, where v is the C4 speed in the absence of current for either the 4-paddler or 3-paddler case. When the C4 is paddled against the current its speed over ground is now v₀ – v. The measured speed over ground will be denoted by v_measured.

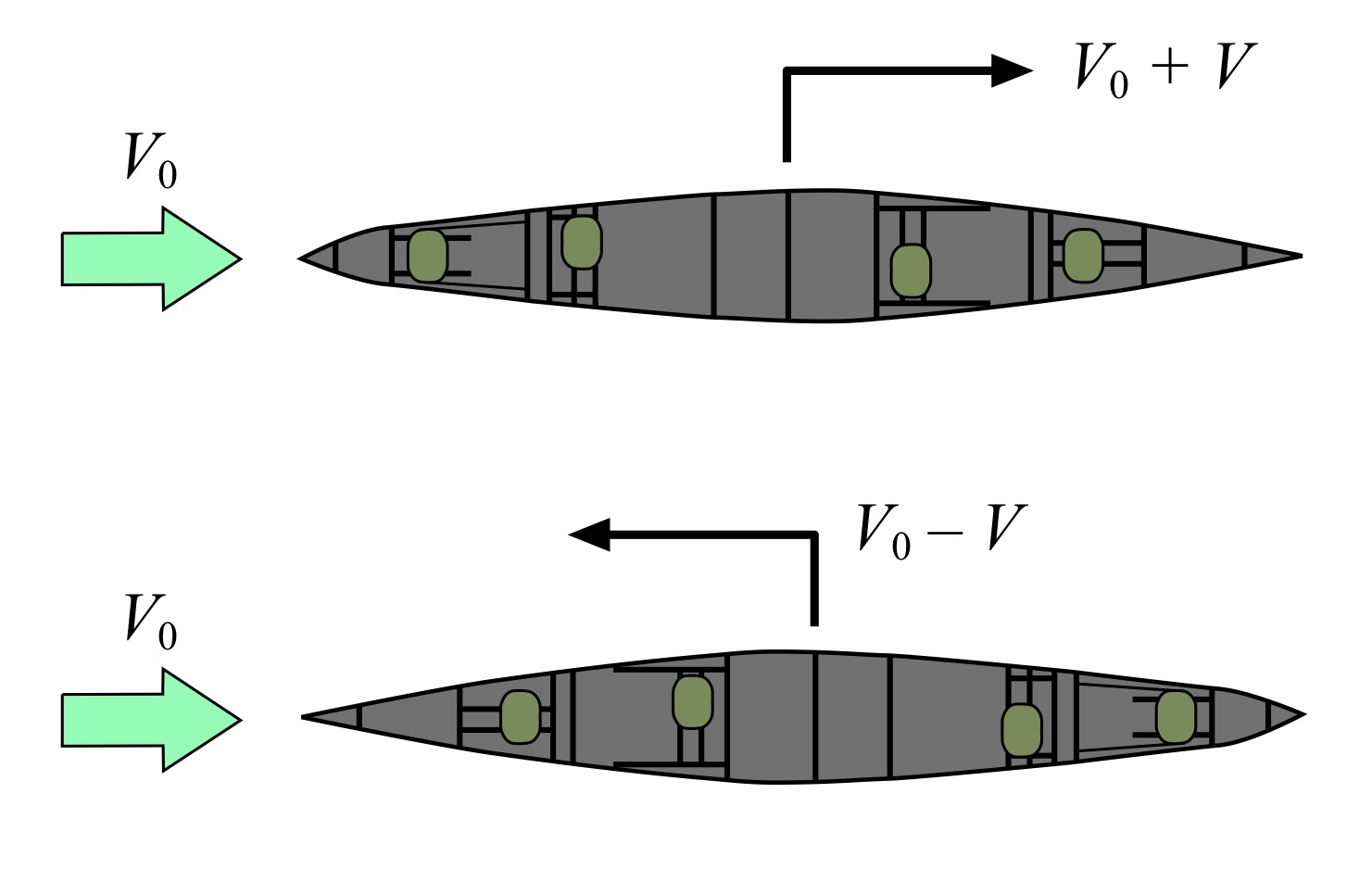
Fig. 2: C4 case, with current.

In order to compute the SAR ratio one needs to know the hull speed attributable to the paddlers, not the measured speed over ground. However, since that speed can be measured both with and against current using a GPS we are given two equations in two unknows, v and V0:

Where the subscripts ‘1’ and ‘2’ denote the with and against current measurements, respectively. Using a little algebra lets us solve for both speeds:

This yields the current-free hull speed v for the 4- and 3-paddler cases. The analysis then proceeds as above.

But… what if the current isn’t directly head-on, or astern? No problem. Let’s assume that the actual current is running abeam to the hull, with speed v_a as suggested in Fig. 3.

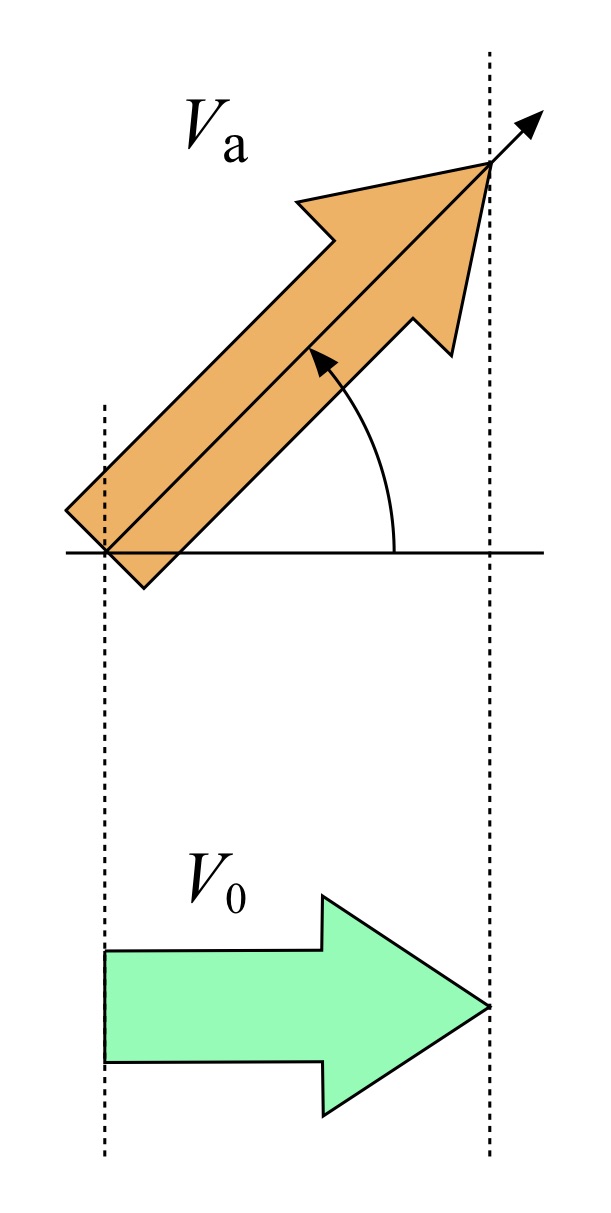
Fig. 3: Current components.

In this plan view the current used in the analysis above still has speed v₀ in the left-to-right direction. The actual current is running at an angle to this, with greater speed. But we don’t care. This is because the component of the actual current in the direction that the C4 will be paddled is still v₀. The speed v₀ is just the cosine of the angle between the actual current’s direction and the boat heading times the actual current speed v_a. Current has a direction, and thus is a vector quantity; we’re just using the component of this vector in the direction that the hull is actually moving. Now obviously this assumes that the current effects the hull equally when running abeam to the bow as well as abeam to the stern, and that the C4’s heading is the same when paddled in both directions. Yes; more things to account for in order to use the SAR ratio accurately and fairly. But subject to all these caveats it can still work.

SUMMARY AND CONCLUSIONS

Subject to a number of caveats and necessary test controls outlined above, we’ve seen that there is a way to quantify a paddler’s performance in an OC-6 outrigger or C4 in comparison to their teammates. Using an analogy from baseball we developed a “Speed Above Replacement” ratio for paddling that could be useful for filling out teams for outrigger paddling, determining which seat is best for a paddler in a C4, etc. The math is simple, and the ratio can be computed using GPS speed data from specific tests as sketched out above.

You probably can’t employ it for C-2s since when paddling bow “solo” it’s difficult to maintain heading; a real-world limitation. And, above a certain number of paddlers the approach breaks down because the SAR ratio will asymptotically approach one, and thus get lost in the weeds in the presence of the real world’s finite measurement precision.

Perhaps the easiest way to characterize paddling power differences is on an erg, or in a C-1 or OC-1 in spite of the fact that working with a team is different than paddling solo. Ergs and C-1s exist, and time over a set distance is easy to quantify. Still, I’ll be curious to see if anyone tries the SAR approach in the field. Let us know if you do!

v1.0

© copyright 2019, Shawn Burke, all rights reserved.  See Terms of Use for more info.

1. The proof is left as an exercise to the reader. C’mon; it’s not that hard! ↑