by Shawn Burke, Ph.D.
INTRODUCTION
OK, so we all know that paddling in shallow water is a pain. You trim aggressively bow down to keep from experiencing that “sinking feeling” in the stern, and paddle like there’s no tomorrow. Yet when you hit the shallows it still feels like you’ve hit a wall. Waves become steeper; your hull speed falls. And heaven forbid if you’re on someone’s inside as you enter a shallow water turn. Hello, shoreline!
So what is it that makes shallow water so challenging to paddle? Why does your hull slow down? Why do waves break toward shallow water and then steepen? More fundamentally, why are the physics governing hulls in shallow water any different than deep water? After all, it’s still just water; right?
Yes, it’s all water. But we inhabit a very particular environment when we paddle: the water’s surface. It is at this interface between air and water that our challenges arise. The culprit is waves. We see waves all around us when we’re on or around water: we watch expanding wave patterns created by a pebble cast into the water; we slowly rise and fall in the long-wavelength swells created by a powerboat on a lake’s far shore; we take a breather by surfing the waves behind another boat during a long race. What dominates paddling resistance at race speeds are the surface waves caused by varying pressures around our hull as it moves through the water. And the fundamental character of these waves begins to change when the depth of water beneath your hull is less than about half your boat’s length.
OF WAVES AND WAVELENGTHS
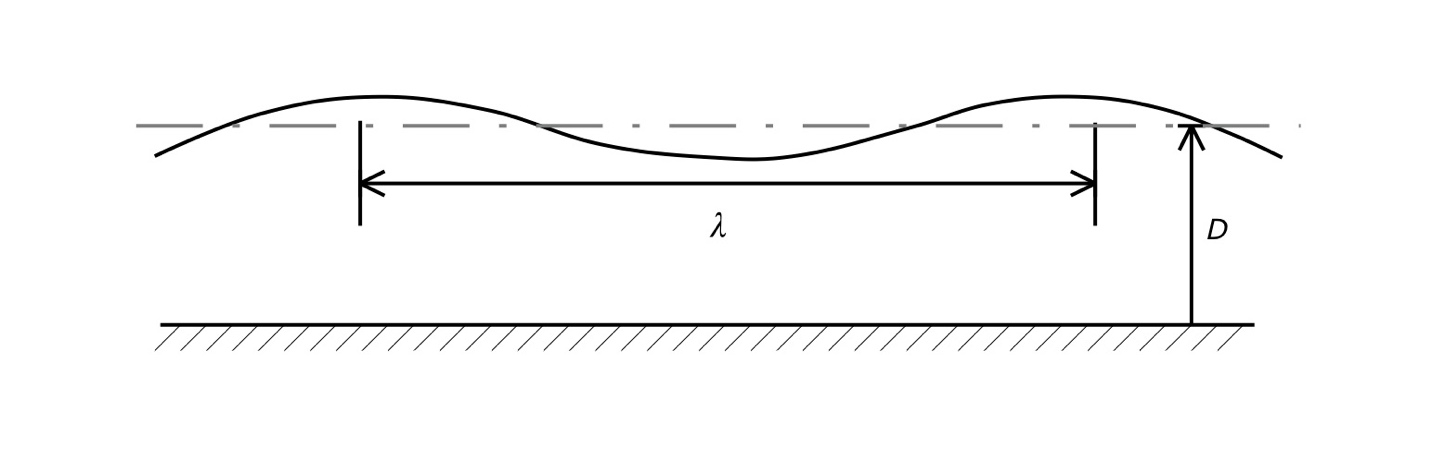
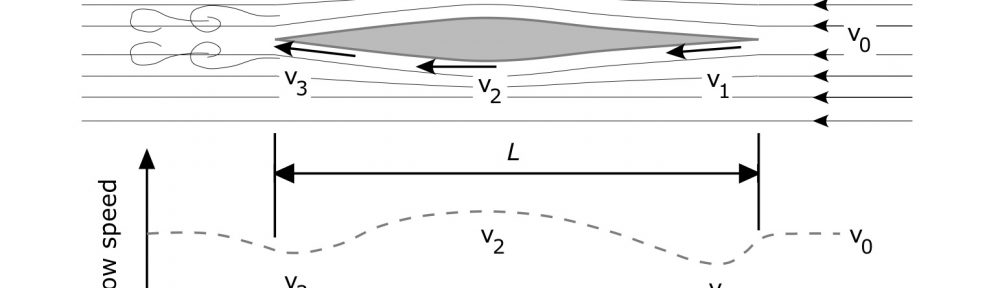
Figure 1: Water and wave geometry.
Now that we’ve let the cat out of the bag, you can proceed to the next article. But if you’re curious about the why, consider waves moving over the surface of water shown in Fig. 1. The water has average depth D. The distance between two wave crests is defined as the wavelength, represented by the Greek symbol λ (“lamda”). We know from experience that waves such as this don’t just sit there, but travel at a certain speed which we represent by cp. There is a relationship between this “phase speed” cp, the wavelength λ, and the depth D,
.
In this equation g is the gravitational acceleration constant and π is the constant “pi” (which equals 3.1415…), and tanh is the hyperbolic tangent function. No need to worry about tanh, as we’ll be looking at deep and shallow water cases where this function reduces to something very simple.
As you can see, the water wave’s speed is a function of water depth and the wavelength – plus a few constants – and nothing else. In other words, wave motion is a property of the water having a free surface, whether there is a boat there or not. And this wave motion must satisfy that relationship: for a given wave speed, there is a corresponding wavelength. The only thing a boat does is provide what mathematician’s call a “forcing function” to the water’s surface, and thus initiate the waves.
When the water is deep, e.g. the depth D is much greater than the wavelength λ, the hyperbolic tangent function reduces to 1. The expression for the phase speed then greatly simplifies to
.
Deep water waves, then, do not depend on the depth D, but only upon the wavelength λ. For the next bit we’ll use this deep-water approximation to guide our analysis.
We’ve all seen the wave train spreading out beside and behind a hull moving across deep water, as depicted in Fig. 2. These so-called “Kelvin Waves” – the same Kelvin after whom the unit of temperature is named – comprise divergent waves spreading out from the hull, and transverse waves that spanning the divergent waves. The wave pattern depends on boat speed. This is because the waves created by the canoe satisfy Equation (2), which relates wavelength λ and the wave’s phase speed cp. As the hull speed increases, the waves created by the hull follow the hull at that same speed. And those waves, which are a property of the water, must satisfy Equation (2). Consequently, the wavelength will increase.
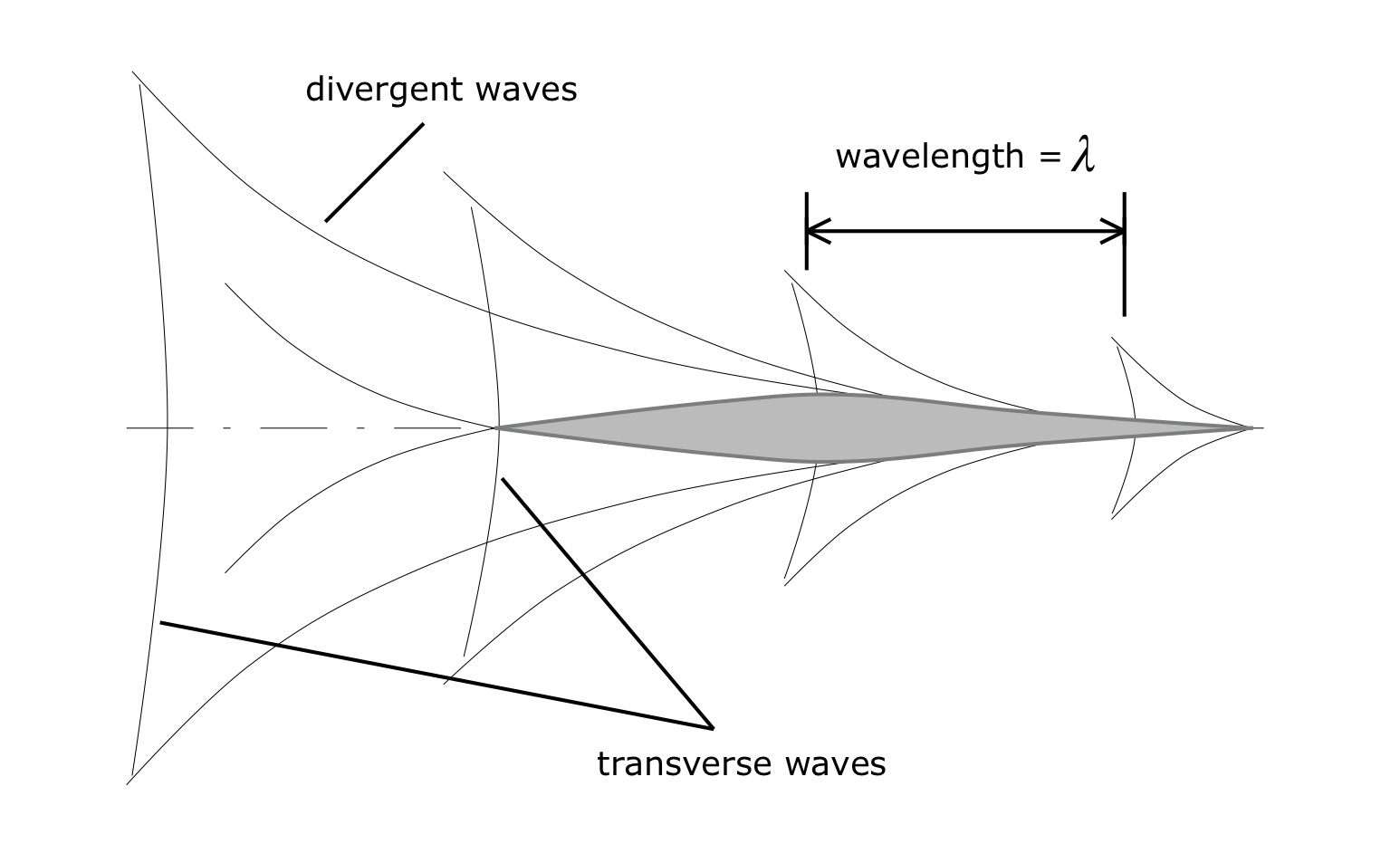
Figure 2: Kelvin waves.
This leads to some interesting wave patterns alongside the hull, as depicted in Fig. 3. This shows a profile view of a USCA C-1, paddled at speeds such that the transverse bow wave’s wavelength is in various proportions to the C-1’s length. In Fig. 3(a) the bow wavelength is half the hull length; this corresponds to a paddling speed for an 18’6” C-1 of about 4.7 mph. As the speed increases to about 5.4 mph the wavelength is now about two-thirds as long as the hull. Then, when the paddling speed reaches about 6.7 mph, the wavelength equals the hull length.
Throughout, the transverse bow wave and stern wave interact. A phenomenon called superposition causes these waves to combine constructively and destructively, leading to the wave pattern shown. There is a trough in the wave pattern around and just aft of midships. As a result, the stern begins to sink a bit, since there is less water to support the rear half of the hull. This is why you need to trim a racing hull slightly bow down even in deep water; when the stern sinks like this the hull becomes less hydrodynamically efficient. (Canoe designers tend to move the hull’s widest point aft of midships to address this shift in buoyancy, as well as to address other hydrodynamic effects.) Finally, as the hull speed surpasses 7 mph, as shown in Fig. 3(d), the superposed wave pattern causes the stern to sink further, requiring significant bow down trim to maintain hydrodynamic efficiency – plus a lot of hard paddling to maintain this sprint speed in a C-1!
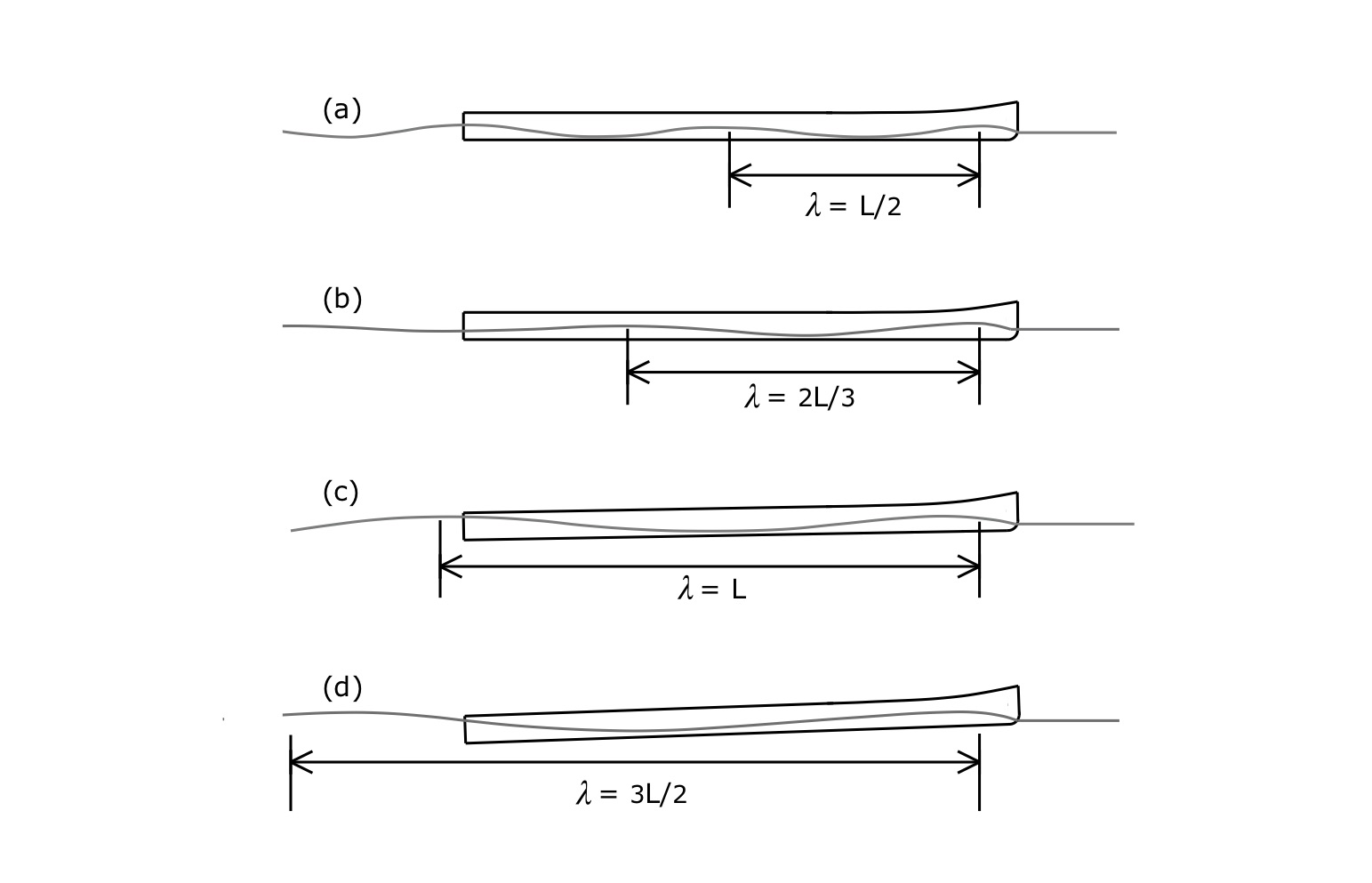
Figure 3: Hull in its own wave train at increasing speeds (not to scale).
The speed where the water wavelength equals the hull length is sometimes called the hull speed. The hull speed, described by Froude in 1868, is a rule of thumb describing the approximate maximum efficient speed for a so-called displacement hull. Since racing canoes and kayaks are (at worst) semi-displacement hulls, this hull speed is not a speed limit, but rather an indication of when wave drag begins to dominate the total drag on the hull. A C-1 can be paddled well beyond 6.7 mph; it just takes a fair amount of fitness to maintain that speed. We can characterize this drag effect using a non-dimensional ratio called the Froude Number. The Froude Number Fr is the ratio of hull speed V to the phase speed cp (which, in the deep water case, corresponds to λ = L):
.
As a rule of thumb, the higher the Froude Number, the greater the wave resistance because of the increasing amount of energy transferred into the divergent waves. The case depicted in Fig. 3(c) corresponds to Fr = 1. When Fr > 1 you’re paddling faster than the phase speed, e.g. faster than the water “wants” to go per Equation (2), hence the increase in overall drag force.
WAVES AND CONSERVATION OF ENERGY
So why does a hull moving through water cause waves in the first place? Perhaps if we could somehow prevent wave creation, we’d escape the effects of wave drag. Unfortunately, like death and taxes, you can’t get around the laws of physics. Waves arise because the shape of the hull – any hull – deflects water. Consider again a USCA C-1 moving at speed V0 as shown in Fig. 4.
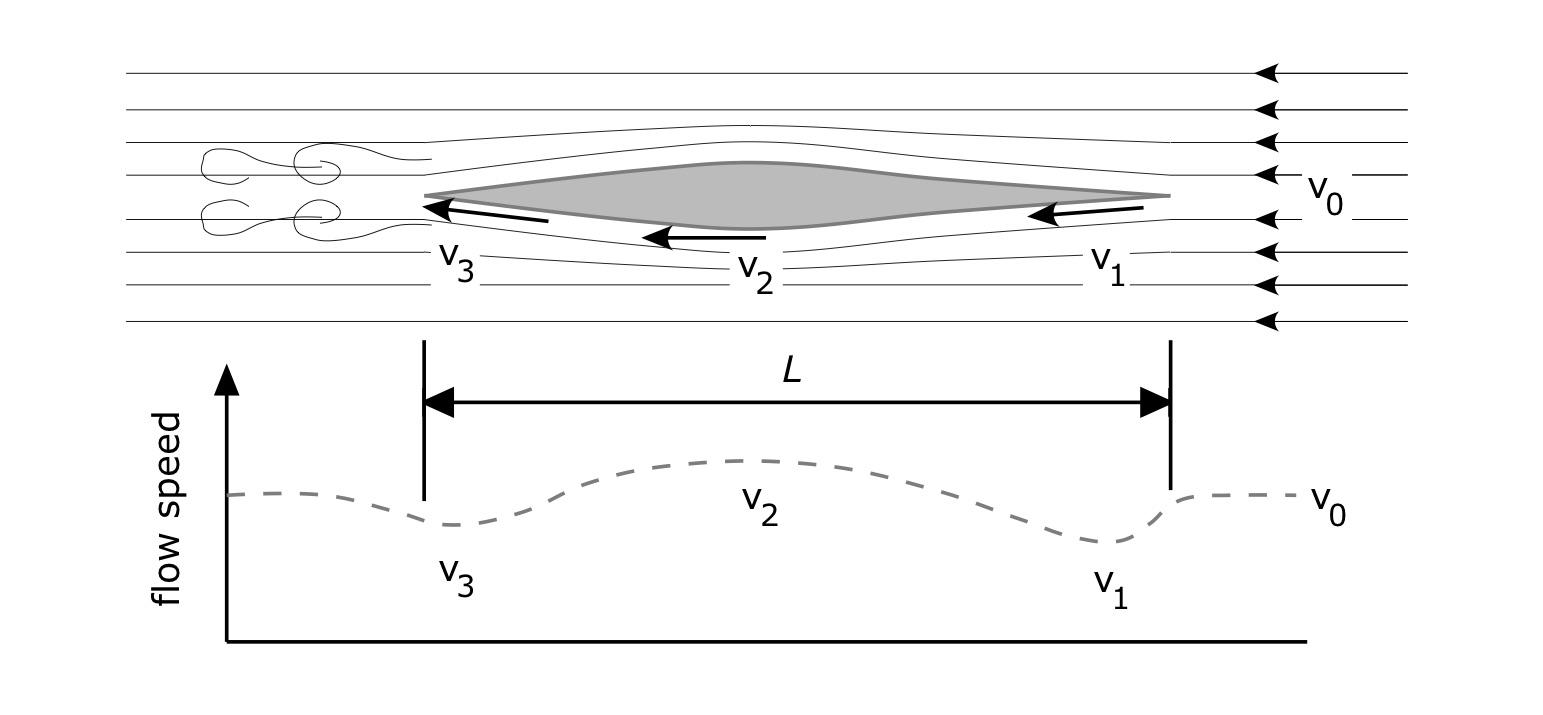
Figure 4: Plan view of flow speeds adjacent to hull (not to scale) and flow speed plot.
Once again, we adopt a paddler-centric reference frame. This means that to an observer sitting in the boat the water appears to approach the hull at speed V0 as they paddle. The water that impinges upon the side of the canoe near the bow slows down a bit to speed v1. As the water continues to flow past the hull, it accelerates a bit around the location of maximum waterline width, reaching a speed v2 that is a bit higher than your paddling speed V0. And finally, as the water flows toward the stern it slows to speed v3, which is a bit slower than the speed adjacent to the bow since some of the water’s energy is spent creating a wake. This variation in flow speed along the side of the hull is depicted conceptually by the dashed line plotted in the lower half of Fig. 4.
The water impinging on the bow has a certain amount of kinetic energy, e.g. energy due to motion. The kinetic energy of a unit mass of incoming water is expressed by
,
where m is the mass of water. Since energy must be conserved, the kinetic energy at location 1 with water speed v1 must equal this “incoming” energy. However, since v1 is less then V0, and energy is conserved, this decrease in kinetic energy at location 1 must be augmented by an increase in potential energy there. Potential energy can be thought of as stored energy. When you throw a ball into the air, the instant it leaves your hand it has a certain amount of kinetic energy. As it rises above you the ball slows, until its vertical speed equals zero. At this precise moment the baseball has only potential energy, which exactly equals the amount of kinetic energy you gave it the moment it left your hand (because of energy conservation). As the ball falls to earth its potential energy is converted back into kinetic energy, and the ball picks up speed. It will return to your hand at the same speed it had when you initially threw it; when it lands it will have the same amount of kinetic energy as when you threw it because… energy is conserved.
Like the ball, water can have potential energy if you lift it up in the air. So the energy at location 1 is written as the sum of the local kinetic and potential energy, which must equal the initial amount of kinetic energy:
.
The height h1 is the displacement of water about the average water depth D as illustrated in Fig. 5.
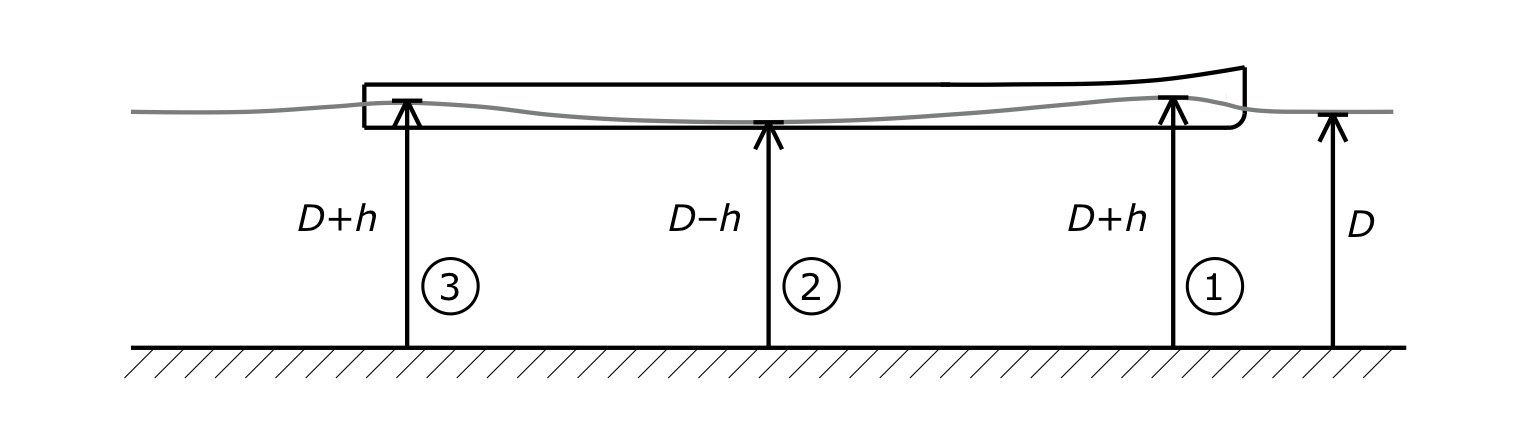
Figure 5: Profile view of hull with hull speed wave train (not to scale).
Conservation of energy requires that the water height h1 be greater than the zero, e.g. the water is displaced above the average depth. A similar result occurs at location 3; since the local water speed v3 is a bit less than v1, the height h3 is a bit lower than h1 yet still higher than the average depth D. Conversely, at location 2 the local water speed v2 is greater than the incoming water speed V0. This means that the kinetic energy at location 2 is greater than the incoming kinetic energy. Since energy is conserved, the potential energy at location 2 must offset this increase in kinetic energy, so that
.
In this case, the height h2 lies below the average depth D; the water is pulled down to satisfy energy conservation.
What does this water profile along the hull in Fig. 5 look like? That’s right: waves. Because your hull deflects and slows water, then accelerates it, then slows it again you create a disturbance in the water. And, since a property of the water is that it “likes” to support and sustain waves, these local variations in water height caused by your hull become the aforementioned forcing functions that drive wave creation. Now designers of modern racing hulls have deduced many crafty ways of minimizing wave creation and wave drag. And these very high performance hulls allow you to paddle well beyond the theoretical hull speed. But the underlying principles still apply: water is still water, your hull displaces it when under way, and the laws of physics still hold.
SHALLOW WATER
Now all of this wave stuff is great, but, when does water become shallow? Isn’t that the point of the article? Indeed it is; we just had to cover the preliminaries. A lot of preliminaries! Time to return to the original expression for the phase speed of surface waves. Previously we had concerned ourselves with the deep water limit, where the hyperbolic tangent function reduced simply to 1. This holds true when the argument of the hyperbolic tangent equals about 3 (you can check for yourself). This means water is considered “deep” when
,
Equating the wavelength λ to the hull length L, this means that water is “deep” when it is deeper than about half the hull’s length.
In the shallow water case, where the depth D now becomes much less than the hull length L, the original expression for the surface wave phase speed simplifies to
.
In other words, in very shallow water the phase speed has nothing to do with the surface wave’s wavelength. It only depends on the gravitational constant g and the depth D. And as the depth decreases, the phase speed decreases as the square root of depth. Things have changed! But what happen in between? Is the transition from deep water behavior to shallow water behavior abrupt or smooth?
We can compute the phase speed vs. depth to answer these questions. We shall assume that the wavelength in Equation (1) corresponds to the length of an 18’6” C-1 running at 6.65 mph. The resulting data is plotted in Fig. 6. As you can see, when the depth equals the boat length, or even about half the length, the phase speed equals the hull speed – the plot stays flat. The phase speed begins to decrease when the depth is about half the hull’s length – as expected give our analysis – and starts to drop significantly when the water depth is approximately one quarter to one third of the hull’s length. This corresponds to what paddler’s refer to as “concrete water,” about 4’ to 5’ deep. As the water depth decreases further, the phase speed drops precipitously. What this means is that the water inherently supports more slowly-moving waves as it becomes shallow. If you try to paddle faster than the phase speed you are providing a forcing function that tries to make the water faster than it wants want to, and you pay the price in wave resistance.
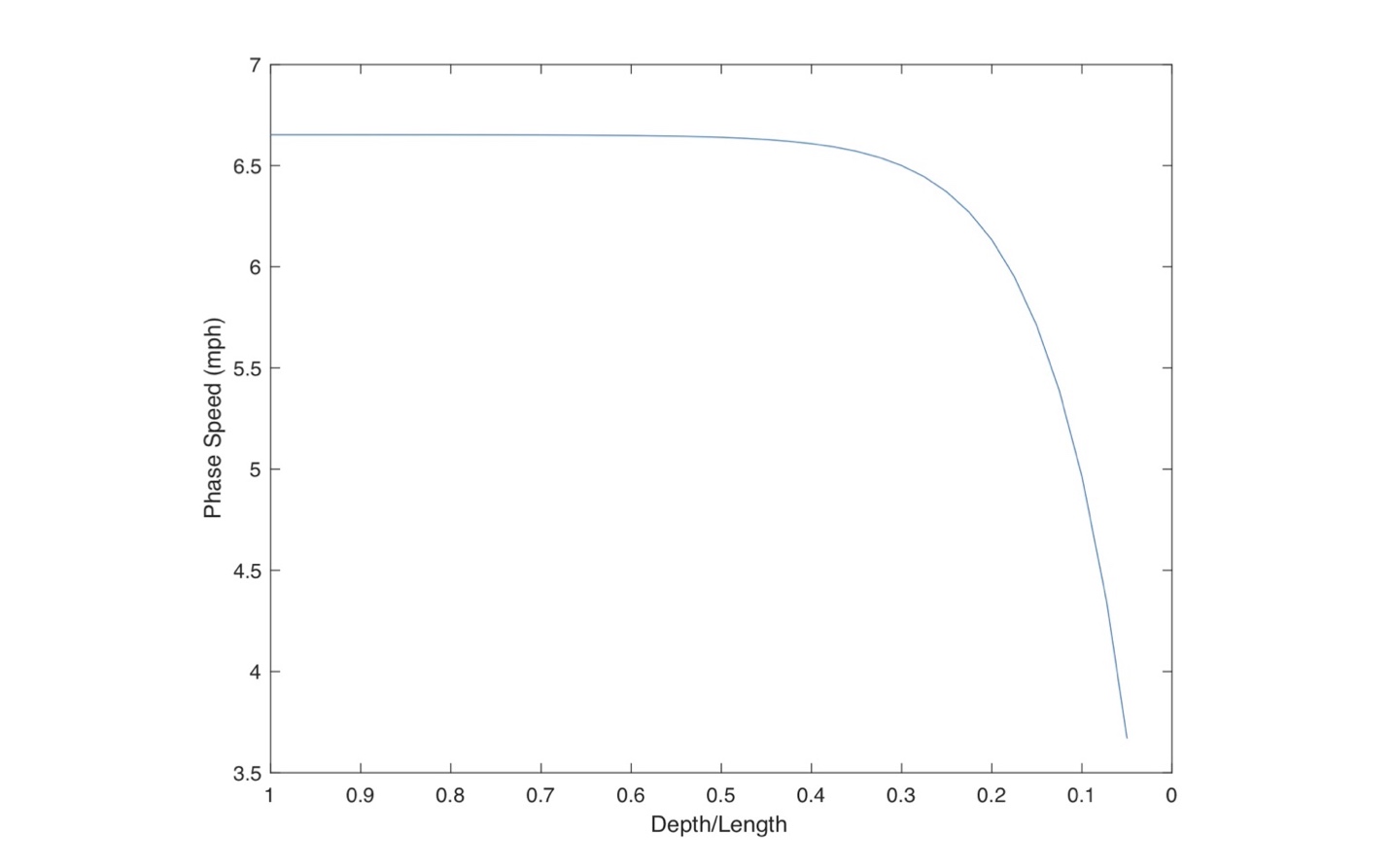
Figure 6: Phase speed vs. depth for an 18’6” hull.
One can appreciate this increase wave drag effect by plotting the Froude Number vs. depth, as shown in Fig. 7. Recall that the Froude Number expresses the ratio of hull speed to the phase speed, and is indicative of increasing wave resistance. Again, we consider the case of an 18’6” long C-1 traveling at 6.65 mph. This suggests that when the water depth drops below 2’, wave drag forces on the hull begin to skyrocket. Sound familiar?
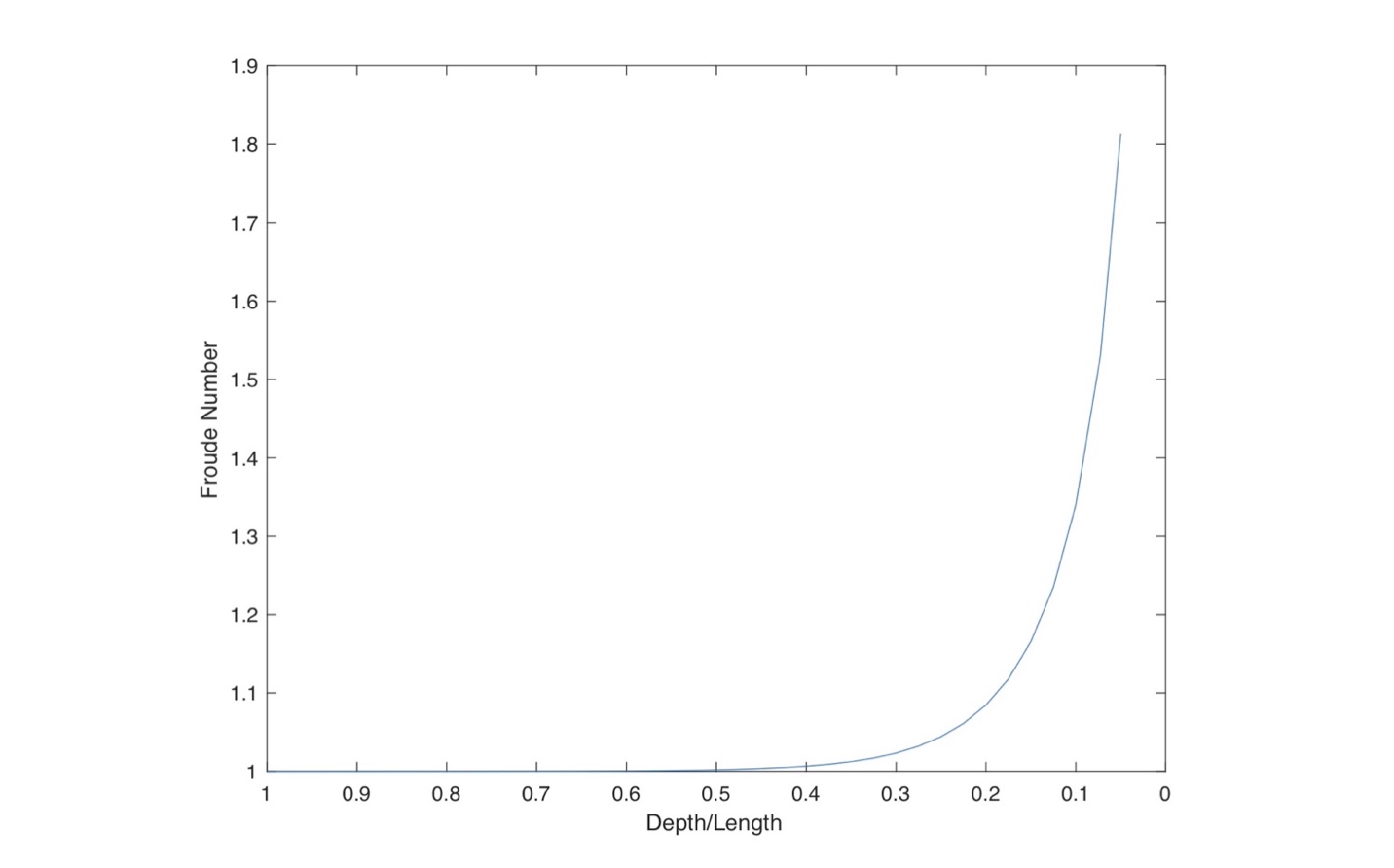
Figure 7: Froude Number vs. depth.
Other factors come into play in shallow water besides decreasing surface wave phase speed. The water beneath the hull becomes “squeezed” between hull and bottom, which are now in close proximity to each other. This causes the water beneath and around the hull to accelerate, leading to a downward suction force on the hull because of Bernoulli’s Principle. This downward suction force is equivalent to having the paddlers suddenly gain weight, as the boat is pulled lower in the water. And as we learned in The Science of Paddling, Part 1, a heavier team is a slower team, everything else being equal, because now you are pushing a larger wetted hull area through the water than before you hit the shallows. Further, in shallow water surface waves grow in height, and eventually nonlinear effects take over – our analysis has been based upon the so-called “small wave” approximation, which soon fails as the wave height is no longer small compared to the water’s depth. At least it was fun while it lasted.
SHALLOW WATER TURNS
And finally, about those shallow water inside turns. Water tends to shallow as you get closer to shore, especially on the inside of river turns. Shallow water effects become more pronounced, then, closer to shore. We have seen in Fig. 6 that the phase speed decreases as water becomes more shallow. One can construct a “map” of wave patterns over the width of a river using this information, as suggested in Fig. 8.
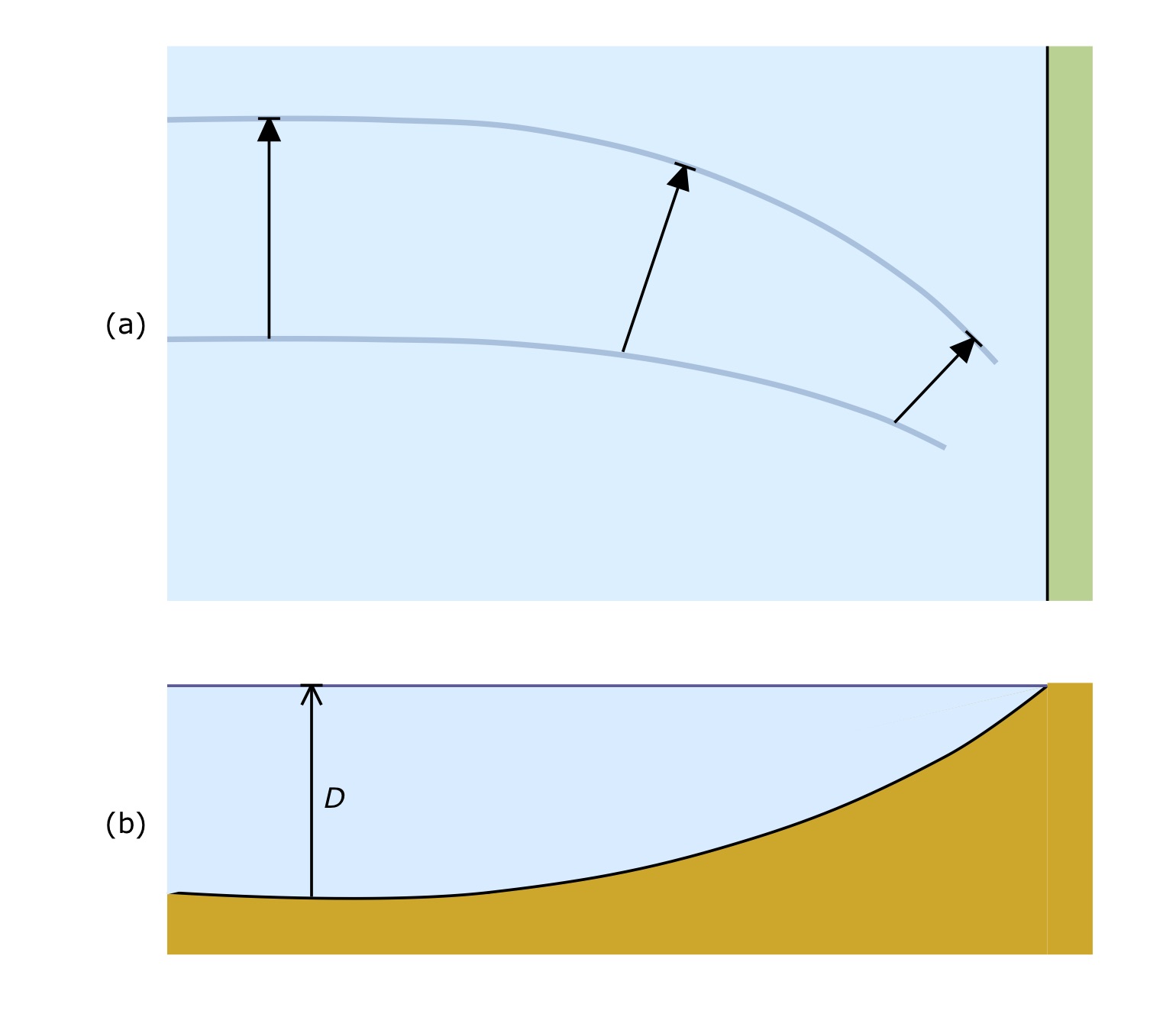
Figure 8: Wave refraction, (a) top view, and (b) river cross section.
In Fig. 8(a) the arrows represent the phase speed at the depth corresponding to their location. A longer arrow represents a greater phase speed; they also span the wavelength of one surface wave cycle. As the water becomes more shallow, the phase speed decreases, as does the wavelength. In order that there be no discontinuities in the wave pattern, the velocity vector must turn toward the shore. Thus the surface waves themselves turn toward the shore as the bottom becomes more shallow there. This phenomenon is called refraction, and is analogous to the bending of light waves at an air/water interface – viewing a pencil in a glass half full of water is a familiar example of this wave bending phenomena, albeit with light waves rather than water waves. So, as the surface water waves bend toward shore, they want to take you with them: toward the shore. And as if refraction wasn’t enough, because the wavelength shortens, the wave heights must increase in order to satisfy conservation of energy. Which is why you want to lead the way into a shallow inside turn, rather than follow on a leading boat’s inside shoulder. Surf’s up!
Version 4.2-B
Copyright (c) 2011, 2017, 2020, Shawn Burke, all rights reserved. See Terms of Use for more information.