by Shawn Burke, Ph.D.
INTRODUCTION
Why aren’t tandem canoes twice as fast solo canoes? I mean all you tandem paddlers have, well, two paddlers. So why aren’t you twice as fast as me in my C-1?
PADDLERS AND POWER
Our canoes move through the water as the result of force we apply through our paddles, with reaction forces transmitted through our bodies into the hull via our torso and legs. This is an embodiment of Newton’s Third Law: For every action there is an equal and opposite reaction. The water exerts a retarding force against the hull known as drag that is constantly trying to slow us down. While the details are rather complex, requiring that one solve vector nonlinear partial differential equations, drag can be thought of far more intuitively as just a force that resists our efforts in linear proportion to velocity at very low speeds, and as a power of velocity at higher speeds.
At very low speeds the drag force experienced by a canoe moving through the water is proportional to the hull’s speed times a friction coefficient. The drag force at higher speeds – and certainly at racing speeds – is proportional to the product of the hull’s wetted area and the square of the speed. The wetted area is the area of the hull beneath the waterline. Since, for example, the width of USCA spec racing canoes is a specified fraction of the length, to first order the wetted area is proportional to[1] the square of the boat’s length. This is because all other hull dimensions can be expressed as a fraction of the length. For example, the width of a USCA Comp Cruiser at the 4” waterline is 14.375% of the stem-to-stem length, etc. Consequently, at racing speeds the drag force is proportional to speed squared times hull length squared.
To compare tandem and solo hulls, let us assume that we have three well-matched paddlers, each capable of exerting the same paddling power. One of these paddlers is in a C-1, while the other two are in a C-2 of equal length that is hydrodynamically equivalent to the C-1.[2] The paddlers’ power is used to overcome the drag forces on their respective hulls to provide forward speed. In other words, the exerted paddling power is proportional to the drag force times the speed. Using the above physical principals, this is proportional to the speed cubed times the length squared. If we denote each paddler’s paddling power as P, the hull speed as V, and the hull length as L, then for the C-1 this relationship between paddler power and speed can be written as
,
where “” means “proportional to.” This relationship can be solved to yield an expression for the speed V in terms of power and length,
.
Thus, the hull speed is proportional to the cube root of the paddler’s applied power. Now for our C-2, which has two paddlers each capable of exerting paddling power P, the relationship between paddling power and speed can be written as
since there are two paddlers, and thus twice the power in the hull. Solving for the speed V,
.
Since the two hulls are the same length L, we see that our tandem will be faster than the solo by a factor of , or 1.26, e.g. about 26%. So to a first approximation, if a C-1 cruises at 6 mph, then a tandem could cruise at 7.5 mph, all other factors being equal. This addresses our initial question: the C-2 does not cruise at double the speed of the C-1 despite having twice the power plant. Tell me something I don’t already know?
ROLE OF WEIGHT IN THE HULL
Now this approximation neglects the effect of the greater weight of the C-2 due to the second paddler. Since the C-2 will weigh about twice the C-1 (racing hulls are light, hence the weight is dominated by the paddlers), it will sink deeper in the water. This increases the aforementioned wetted area of the hull, which should slow the C-2 a bit and make the C-1 and C-2 a bit closer in cruising speed. We’ll deduce the impact of paddler weight as we consider our next question: If I lose weight, will I go faster?
Paddling a canoe can be thought of as moving a hole through the water. This hole is created as a result of water displaced by the hull. The total weight of the paddler(s), plus the weight of the canoe and gear, equals the weight of the water displaced by a loaded hull – this is Archimedes Principle (“Eureka!”) assuming, of course, that you’re afloat. If the weight of the paddler(s) increases, the amount of water displaced increases.
Since the weight of the displaced water equals the density of water times the displaced volume of water (submerged length width height, a cubic dimension), we see that to first order weight is proportional to the length of the hull cubed.
As you paddle your “moving hole,” water is continually rushing in behind the hull to fill the hole it just left behind. This is why wake riding works: you are essentially pulling along a chunk of water as you paddle, which a waking canoe can sit in. The mass of this moving hole increases in proportion to the amount of water displaced by the hull, which is linearly proportional to the weight of the paddler(s) because of Archimedes Principle.
From Newton’s Second Law, the force you exert to accelerate a canoe is proportional to the mass you wish to accelerate. So, if your weight increased in the off-season by 5%, then you must apply 10% more force to accelerate your C-1 to the same cruising speed as last year. Why 10%, and not 5%? Because you must accelerate not only your (expanded) mass, but also the increased mass of water entrained by the hull – a heavier paddler displaces more water, which you have to pull along with you. So that 5 pounds you gained from all that Christmas cheer will actually cost you around 10 pounds on the water the next time you try to jump a wake. A 10-pound weight gain will cost you around 20 pounds, etc. And since the hull slows down ever so slightly between each and every stroke, you are slightly accelerating the hull with every stroke just to keep it at cruising speed. Makes you think twice about that second helping of stuffing…
But wait; there’s more!
Recall that the drag force on a hull is proportional to the wetted area times the square of the hull speed. Since the wetted area is proportional to the length squared, and the cube of the length is proportional the weight W of the displaced water, then
.
Thus, the relationship between power and speed can be written in terms of the paddler(s) weight as
,
which, solving for the speed V yields
.
So for a fixed amount of paddling power, hull speed goes as the –2/9 -th power of weight, and the cubed root of paddler power. Not exactly an intuitive relationship, eh? But plugging in a few numbers will provide some insight into how important each effect is.
For example, if a paddler gains 5% of their weight eating cookies and eggnog over the winter months, but doesn’t lose any paddling power, then their cruising speed will decrease to , e.g. a drop of 1 percent. If that same paddler did a tad too much carbo loading and instead gains 10% over their ideal weight, then their cruising speed will decrease to
, e.g. a drop of 2 percent. Doesn’t seem like much, but a 2% decrease in cruising speed means that a race they paddled last year in 1 hour will now take 1:01:13, which in canoe racing can certainly can equal the margin of victory.
Fig.1 shows the range of impact on race time on a hypothetical 1-hour long race of increasing paddling power, and of decreasing paddler weight.
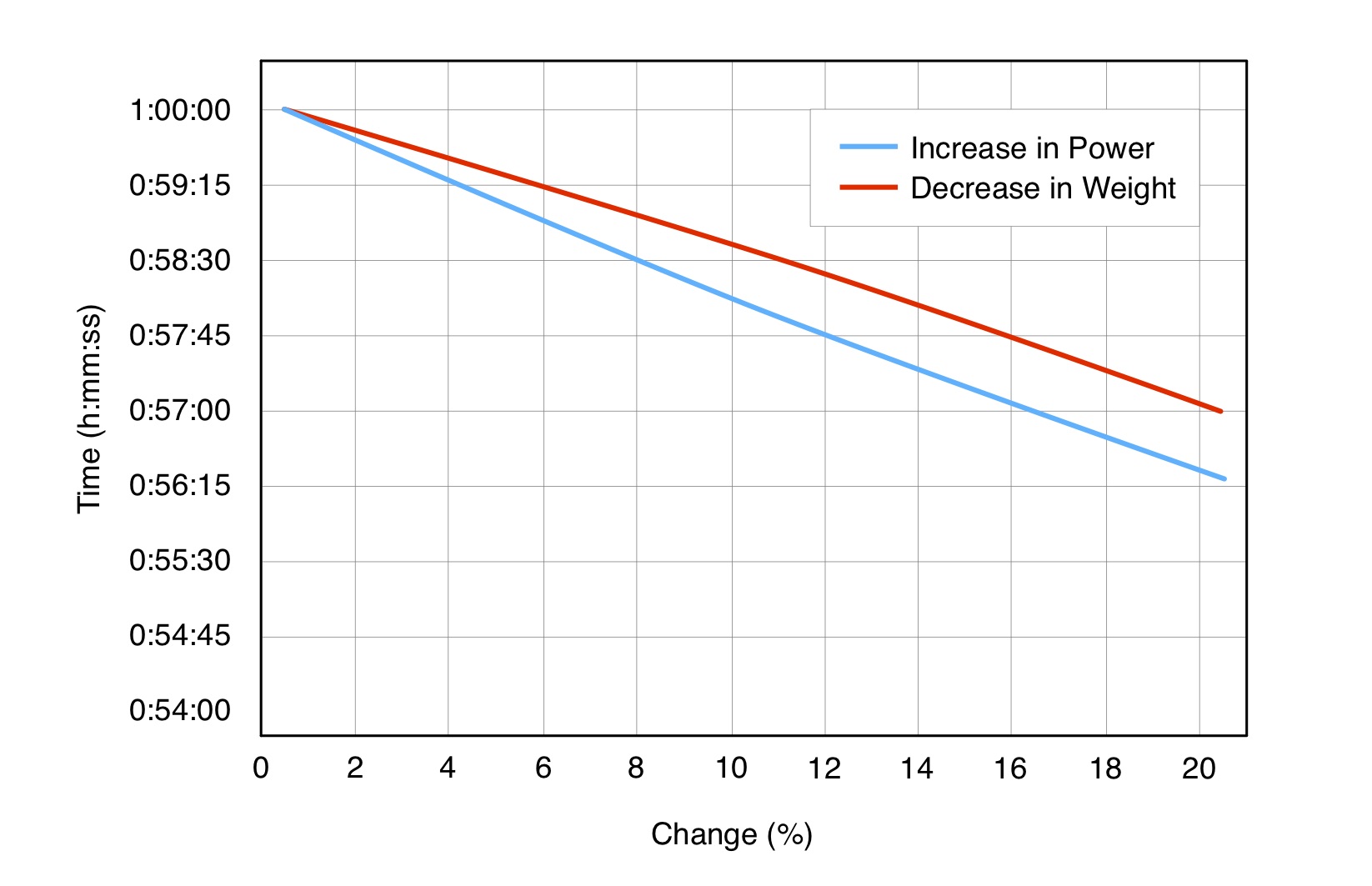
Figure 1: Impact of Power and Weight on Race Time.
Returning to our C-1 vs. C-2 paddler discussion, let us now assume that all three paddlers not only have the same paddling power, but they all weigh the same as well. Since marathon paddlers paddle lightweight hulls, the weight of the paddlers will be significantly larger than the weight of the canoes. The tandem canoe plus its paddlers will then weigh about twice the C-1 and its paddler. This 100% increase in weight will decrease the tandem’s cruising speed to . So, while we expected that the tandem’s double power plant would be about 26% faster than an equivalent C-1 and paddler, we see now that the increased wetted area of the tandems hull will decrease this power gain to 1.26 x 0.86 = 1.08, yielding an 8% advantage in speed over a C-1. If a C-1 can paddle a course in an hour, an equivalent tandem could paddle the same course in about 0:55:30, assuming all other factors are equal; if a C-1 cruises at 6 mph, then a tandem with power-equivalent paddlers would cruise at ~6.5 mph. This result is far more reasonable in light of real-world results than the 26% difference calculated from the difference in power plant alone.
The question now is, which should a paddler focus on: gaining power, or losing weight? We see from the above that cruise speed is related to a type of power-to-weight ratio:
.
The expression in parentheses shows that the impact of increasing paddling power P is greater than of decreasing a proportional amount of weight W because of the cube and square, respectively. Developing paddling-specific power will pay off a bit faster than losing weight. And paddlers with an excellent power-to-weight ratio will perform the best of all. That’s why many female paddlers, and many light mixed teams, do so well at the races.
Another way to look at it is, should I lose weight, or trade in my standard-weight hull for an ultra-light hull? Wouldn’t the effect be the same? Here, we can do some simple financial modeling. Say the cost of a health club membership is around $10 US per week. One can sustainably lose about 1.25 pounds per week through proper diet and exercise. If you need to drop 10 pounds, you can do this in about 8 weeks. At $10 US per week this leads to about $80 US in health club membership fees. Compare that to the $500+ US you’ll pay as the premium for an ultra-light hull, and you’ll see that going to the local health club to lose the weight is more cost effective… and may increase your power to weight ratio to boot!
V1.2-B
© Shawn Burke, 2008, 2020, all rights reserved. See Terms of Use for more information.
Excellent article, Shaun.
Have you studied the effective power output of the various canoe paddle stroke techniques?
Mike Malley
Hi Mike! Thank you for the kind words. It would be fun to compare and contrast the various strokes: marathon, outrigger, and sprint on the single blade side. But since I write these articles for fun, without external funding, that may not happen soon. I do have some preliminary analysis on the interrelation of stroke force, power, and energy expenditure that builds on the last half of “Part 5: What Moves You.” I’ll to return to that in the (hopefully) not too distant future. Thanks for the feedback! — Shawn Burke