by Shawn Burke, Ph.D.
NOTE: This article is being re-written to more accurately address paddler synchronization. I now have access to Matlab and intend to perform a series of simulations for tandem, C-4, and other multi-paddler hulls.
Perhaps the first paddling truism I ever learned is that tandem paddlers must always paddle in sync with each other. Recently, I began wondering whether there really was any truth to that old saw. It turns out that there is, and the underlying reasons are both obvious, and unexpected.
We’ve all seen tandem canoes that pitch and bounce down the course. This can be due in part to poor paddler synchronization. But a pitching tandem it is more often than not the result of poor stroke mechanics, including excessive body motion, an overly long stroke that pulls down the hull, or poorly matched partners. To zero in on the effects of paddler synchronization alone, we’ll assume that we have well-matched tandem paddlers with good mechanics, and focus instead on how stroke synchronization effects force transfer in moving the hull forward.
First we need to understand what happens when you perform a paddling stroke. As you perform a forward stroke the blade’s power face exerts a force on the water. The canoe moves forward in response to the stroke, which is an embodiment of Newton’s Third Law: For every action there is an equal and opposite reaction. The force on the blade is zero during the recovery phase when the paddle is out of the water. The force then grows over time to some maximum level during the stroke’s power phase. As the power phase ends, and you prepare to remove the paddle, the force decreases, once again reaching zero when the recovery begins. If you’ve ever been on a paddle ergometer with a performance monitor display, you’ll be familiar with the following type of plot of paddle forces over time:
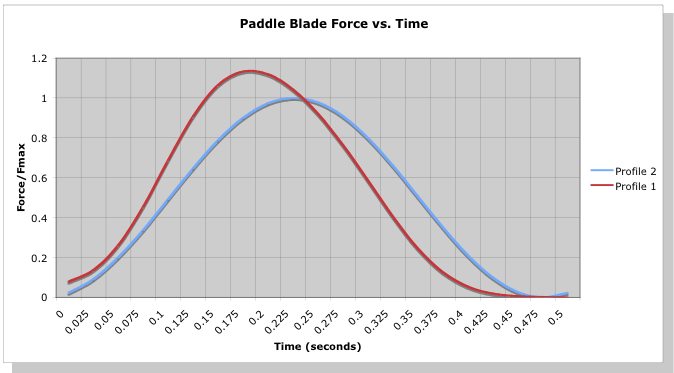
Figure 1: Paddle blade force vs. time.
In Figure 1 there are two force curves. The first (red) curve represents a forceful early pull on the paddle right after the catch. The second curve represents a slightly “smoother” acceleration of the paddle resulting in maximum force around mid-stroke. You’ve probably performed both types of strokes, and we’ll revisit the differences and advantages of each in a later article. But for now the primary take-away is that during the stroke’s power phase the force on the paddle’s blade after the catch grows over time to some maximum value, then decreases back to zero. We’ve chosen the peak amplitude of each blade force profile such that the area under each curve is equal, which to a first order approximation means each stroke exacts the same amount of work from the paddler. More on this later.
Since we wish to understand the underling physics rather than futz with trigonometry, we can simplify the force curves of Figure 1. Consider the paddle force vs. time curve shown in Figure 2:
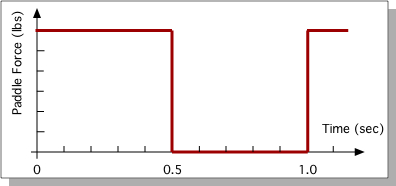
Figure 2: Idealized paddle force vs. time.
This represents an idealized paddle force profile. We’ve simplified the stroke force profile to be a simple on/off pattern: the paddle is either in the water pulling (paddle force “on”), or the paddle is out of the water (paddle force “off”). We’ve further simplified the stroke to have the power phase duration equal to the recovery phase duration. This makes the analysis a good deal simpler.
Now consider two tandem paddling scenarios. In the first, our paddlers’ strokes are perfectly in sync. In the second they’re “perfectly” out of sync. Comparing these two scenarios will allow us to most easily identify the reasons to sync up.
Consider first the tandem team where each paddler paddles perfectly in sync with the other. The combined average paddle force they apply over the stroke corresponds to the “In Sync” on/off curve in Figure 3. Next, consider this same paddling duo, but now each paddler alternates their power and recovery phases with the other. Since we’ve assumed that the power and recovery phases have equal length, the average paddle force applied to the water is now constant: first, the bow paddler takes a stroke, and immediately as their stroke ends the stern paddler takes their stroke, and so on. This is depicted in the “Out Of Sync” line in Figure 3. By paddling exactly out of sync with each other this idealized tandem pair is applying a constant force over time to the water through their paddles, hence the straight line[1]. These two scenarios represent the most two paddlers can be in sync, or the most that they can be out of sync. In one case the peak force in the water is higher, but only for half of the time; in the other there is always an applied paddling force. The question is, which leads to a faster boat?
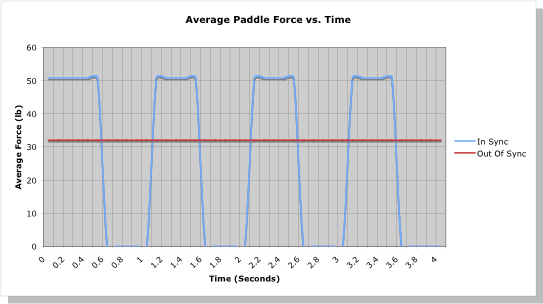
Figure 3: Idealized combined tandem paddle forces vs. time.
We can answer this by calculating the speed achieved in each scenario. We’ll make a couple of additional assumptions to keep things simple: (1) The canoe is assumed to already be up to speed in each case, cruising at a decent clip; and (2) The canoe is moving fast enough that we can focus on form drag, and neglect friction (aka “viscous”) drag forces on the hull. This latter assumption is borne out in Figure 4, which is a plot of the drag force exerted on a tandem canoe hull by the water as a function of hull speed.
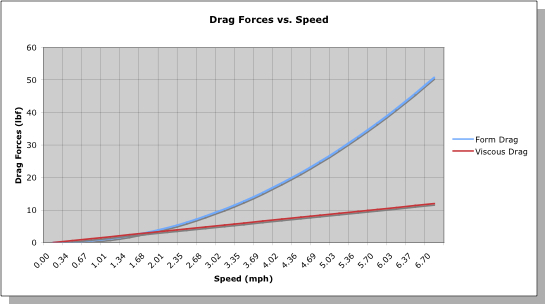
Figure 4: Example drag force vs. hull speed.
The drag force on a canoe hull is the sum of all forces acting on it due to the water as you paddle. At very low speeds, we see that friction drag is as important as form drag. However, since form drag increases as the square of the hull speed, it quickly dominates the total drag, especially at race speeds.
Given all that, we can develop a mathematical equation that relates the total paddling force F to the drag force in terms of canoe speed V using Newton’s Second Law – the sum of the forces acting on the hull must equal to the total mass of hull plus paddler times the hull’s acceleration:
.
In this equation, m is the mass of the canoe plus paddlers, L is the canoe’s length, and CD is a drag coefficient that is specific to the hull design. The term dV/dt signifies the rate of change of the canoe’s velocity, otherwise know as the canoe’s acceleration[2]. This relationship is called a “governing equation.” Solve it, and you can predict the canoe’s speed V as a function of time t given how the paddle force F varies.
Now our little equation looks unassuming enough. However, geeks like me recognize it to be a nonlinear ordinary differential equation. Yikes! Oftentimes, a nonlinear equation like this causes engineers’ knees to shake, their hands to tremble, and has converted a lot of prospective engineering students into economics majors. But a little paddling insight will help us tame this beast.
We know that during the initial portion of the stroke’s power phase the canoe accelerates. Once it comes up to speed during the power phase, the canoe achieves – at least momentarily – a steady-state velocity. During the stroke’s recovery phase it decelerates due to drag forces on the hull, as there is no paddle force to help it maintain speed; the water is always trying to slow you down. In the steady state, since there is no acceleration or deceleration the derivative term vanishes, and the paddle force F and hull speed V are in equilibrium via the relation plotted in Figure 3. Consequently,
.
Once you know the drag coefficient CD, and the total average paddling force F from Figure 2, you can compute the canoe’s speed at the end of the stroke’s power phase. We’ll do that in a minute.
When the paddles are out of the water, the paddle force F is zero. This makes our governing equation a snap to solve… at least if you’re familiar with these types of things. As a result, during the recovery phase the canoe’s speed V can be written as a function of time t as follows:
.
You can see from this equation that since the velocity V is inversely proportional to time t, the hull will slow down over time in the absence of another paddling stroke. Yay, physics! Referring back to our two paddling scenarios, for the paddlers perfectly in-sync, the canoe’s speed will be roughly constant, then as per the equation above it will decrease as 1/t until the next stroke. For the paddlers that are perfectly out-of-sync, the speed will always be constant because the force is constant. Plugging in the numbers, the results for canoe speed for our two scenarios is plotted in Figure 5.
During the power phase, the in-sync paddlers achieve a speed of about 6.7 mph, a good clip for a C-2. During the recovery phase, the speed dips, but not all that much over our half-second recovery (assuming a stroke rate of 60 strokes per minute, and a power phase that is equally as long as the recovery phase). In comparison, our perfectly out-of-sync paddlers only achieve a speed of about 5.3 mph. Why?
Going back to Figure 4, which relates hull speed to the drag forces on the hull, we see that a higher total paddle force will put the canoe “further up the curve” of force versus speed, resulting in a higher steady state hull speed. The out-of-sync paddlers, while always exerting a force to move the boat, never “climb the curve” as far since their combined paddling force is only equal to the force of one paddler at a time; with each stroke, the canoeist not paddling is just dead weight. Even though in our example the in-sync paddlers have a recovery that is equal in length to their power phase, the boat never slows down enough when coasting between strokes to make it slow enough to dip below the steady state speed of our out-of-sync paddlers. The greater combined paddling force of the in-sync paddlers wins.
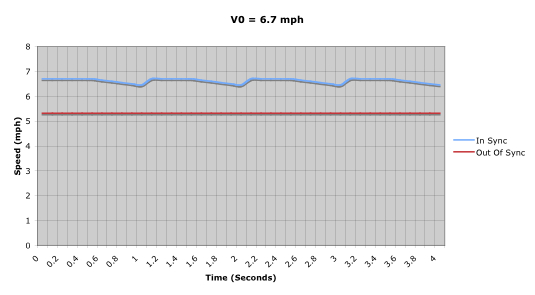
Figure 5: Hull speed over time for two scenarios.
Now these examples were chosen to exaggerate the differences between paddling in sync and out of sync so that we could deduce the underlying physics. Realistically, nobody is going to paddle a tandem completely out of sync – each stroke is equivalent to paddling a C-1 with an extra paddler lounging in the hull! And the paddle stroke recovery time is going to be a fraction of the power phase duration for all paddlers. As we do this, the differences between the curves in Figure 4 become less and less. But one can show that the optimal solution to our governing equation is to have the paddlers paddle perfectly in sync.[3] So to go faster “climb the curve” as far as you can (paddle in sync to maximize combined paddle force to overcome the drag forces on the hull), and don’t coast too long (speed up the recovery).
Now more particularly, how important is it to not only match tempo bow and stern, but to match stroke force profiles? The analysis above showed the importance of matching strokes to maximize the summed force of the tandem paddlers. But what if our strokes are not idealized square waves, but realistic strokes like those shown in Figure 1? The answer is found simply in terms of the sums of these more realistic paddle blade force profiles, as shown in Figure 6.
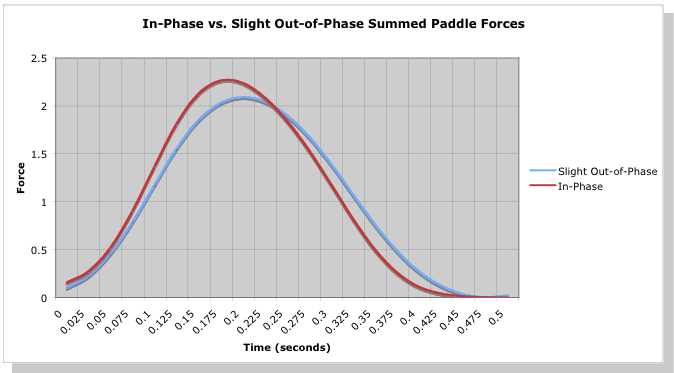
Figure 6: Summed paddle force profiles for in-phase and slightly out-of-phase strokes.
The “In-Phase” curve in Figure 6 is the sum of two copies of the first stroke profile shown in Figure 1, e.g. the “front-loaded” force curve. The “Slight Out-of-Phase” curve in Figure 6 is the sum of the two different force curves in Figure 1, e.g. a “front-loaded” stroke and “mid-loaded” stroke. You can see that the sum of the matched stroke profiles achieves a greater peak force than the sum of the slightly mismatched stroke profiles. The result is that this perfectly matched pair will “climb the curve” of drag force vs. speed a bit higher (higher speed during the power phase) than the slightly mismatched pair, resulting in a bit more speed. So we see that no only does a tandem pair need to paddle in sync, but to maximize their speed it is best to have paddlers whose stroke force profiles match in time as well.
I guess some old saws become old because, well, they’re true. Tandem paddlers should paddle in sync. Really in sync!
- The amplitude of the average paddle forces shown in Figure 3 differ by a particular amount. I’ve chosen the average peak force of the in-sync pair, and the average force of the out-of-sync pair, such that the power exerted by the paddlers is the same over time over the course they paddle. This means the force values differ by about a factor of 1.26. I could have chosen a simple factor of two, but this will serve to make our point just as well. ↑
- This is also called the “derivative” of the velocity V; snuck a little calculus in, and it didn’t hurt a bit, did it? ↑
- The result is expressed in terms of Mathieu functions, which are not for the faint of heart – just take my word for it. ↑
Copyright (c) 2017, Shawn Burke. All rights reserved. See Terms of Use for more info.
(v2.1)
