by Shawn Burke, Ph.D.
So which is faster: paddling an out-and-back course without current, or with current? You lose time going upstream into current, but you regain it going downstream… don’t you? A round trip should take the same amount of time, right? Well, read on.
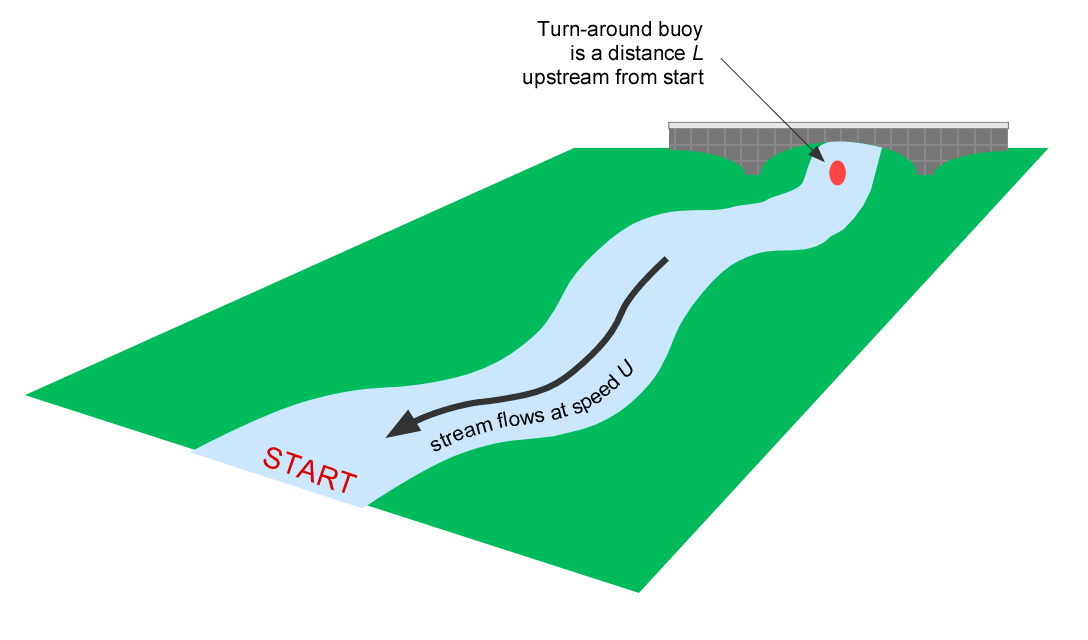
Consider an out-and-back course that first travels upriver, then back downriver to the starting point. If the one-way distance to the turnaround buoy is L, then the round-trip distance is twice this, or 2L. When there is no current, and you paddle this course at speed V (and, unlike me, could magically make the buoy turn in zero time), then your round-trip paddling time Tstill would equal
Now let the river have everywhere a uniform current, with speed U. This means your upstream speed will now equal V – U, e.g., the current slows you down. As a result, your time to the turnaround buoy Tup is now
As you can see, since your upstream speed (V – U) is less than your still water speed V, your time to the turnaround buoy Tup is now greater than in still water due to the river’s current. Nothing new there, eh? Good.
With current, your downstream speed will now equal the sum of your quiet water paddling speed V plus the speed of the current, V + U. As a result, your time from the turnaround buoy back to the start, Tdown , will equal
As expected, since your downstream speed (V + U) is greater than your still water speed V your downstream time will be faster than if there was no current. Again, nothing new.
With current, your round-trip time is the sum of your upstream time Tup and your downstream time Tdown,
Using our expressions for Tup and Tdown, and a bit of algebra,
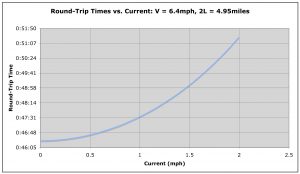
This relationship is plotted in the Figure below for V = 6.4mph, and 2L = 4.95 miles[1]. The no-current round-trip finishing time is 0:46:24. Note that if the river had no current, U = 0 and Tcurrent = Tstill; check. However, if the current is non-zero, then Tcurrent will always be greater than Tstill, since the denominator of Tcurrent will always be less than V – the term in parenthesis in equation (7) is always less than one. As a result, on an out-and-back course that travels up and then down a route with current, you can’t recover the time lost going upstream on the faster downstream leg. The time relationship is not linear with speed, both for each leg as well as the total time.
 If the current is much slower than your quiet water paddling speed, U << V, the term U2/V2 in the denominator of equation (7) is much smaller than 1. In that case you can use a binomial expansion to approximate equation (7) as
If the current is much slower than your quiet water paddling speed, U << V, the term U2/V2 in the denominator of equation (7) is much smaller than 1. In that case you can use a binomial expansion to approximate equation (7) as
For non-zero current speed U, the term U2/V2 is greater than zero, which means 1 + U2/V2 is greater than 1. Your round-trip time will always be slower in the presence of current, no matter what. Going faster on the downstream run because of current will not make up for going slower on the upstream run. It’s like death and taxes: you can’t win, you can’t break even, and you can’t get out of the game.
There are two other limiting cases of interest: If the current is running as fast as you can paddle, e.g., U = V, then Tcurrent becomes infinite (see the fifth equation above); you never get to the turnaround buoy… or anywhere else for that matter, as you’d just be sitting still in the Earth’s reference frame. If the current is going faster than you can paddle, e.g., U > V, then Tup becomes negative – you’re going backwards… but not back in time! (Or have we invented a time machine… ?)
Is the fact that you “lose” round-trip time when there is current all that surprising? Not really, if you change your perspective. We habitually think of the round-trip transit problem in terms of distance, since we remember that distance equals velocity times time, or in terms of speed. For a fixed time, if we double the speed, we go twice as far. But for a fixed distance course, time and speed have an inverse relationship. As a result, even when there is no current the relation between round-trip course time and boat speed is not a simple linear proportionality, as shown in the Figure below.
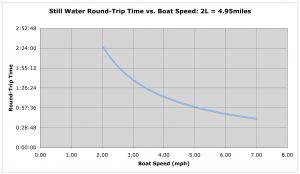
This curve “flattens out” at higher boat speeds, reflecting a more linear proportionality the faster you go. A faster boat speed means the effect of current on round-trip course time is reduced, not eliminated.
The only way to make up the time deficit is to paddler faster than the still water speed V on one of the legs. If you’re racing you’d naturally pick up the pace over the last downstream mile or so, right? But, alas, paddling faster on one of the legs violates a key assumption of this analysis; we assumed that V would be constant. This is a nice example of how one must always keep the underlying assumptions in mind when considering the conclusions of any study or article such as this one.
AFTERWORD
While writing this article I was reminded of a problem noted at the Rio 2016 Olympics. It turned out that the swimming pool may have had some current in the high numbered lanes. (See, for example, https://www.theguardian.com/sport/2016/aug/18/olympic-pool-current-swimming-results-rio-2016.) Swimming events are timed no more precisely than 0.01sec (ten milliseconds) because pool walls are only so flat; these irregularities in lane length correspond to about 5 milliseconds of time at 50m freestyle swimming speeds. In light of the analysis above, a slight bit of current in the pool could have had as large an impact on timing round-trip swimming events 100m in length or longer as irregularities in pool shape.
Copyright (c) 2017, Shawn Burke. All rights reserved. See Terms of Use for more info.
- A distance familiar to those of us who used to paddle Wednesday nights on the Charles River. ↑